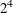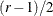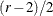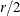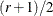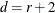You use the MODEL statement to provide the model for the construction of the factorial design. The model can be specified
either directly by specifying the effects to be estimated with the ESTIMATE= option or indirectly by specifying the resolution
of the design with the RESOLUTION= option.
Note: If you create a fractional factorial design or if you create a design that involves blocking, the MODEL statement is required.
The two model-specifications are described as follows:
-
ESTIMATE=(effects) <option>
-
identifies the effects that you want to estimate with the design. To specify effects, simply list the names of main
effects, and join terms in interactions with asterisks. The effects listed must be enclosed within parentheses. See the section Specifying Effects in the MODEL Statement for details. You can use EST or E for the keyword ESTIMATE.
After the ESTIMATE= option, you can specify the following option:
-
NONNEGLIGIBLE=(nonnegligible-effects)
-
identifies nonnegligible effects. These are the effects whose magnitudes are unknown, but you do not necessarily want to
estimate them with the design. If you do not want certain effects to be aliased with ESTIMATE= effects, then list them in
the NONNEGLIGIBLE= effects. The nonnegligible-effects listed must be enclosed within parentheses.
You can use NONNEG or N for the keyword NONNEGLIGIBLE.
For example, suppose that you want to construct a fraction of a 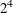 design in order to estimate the main effects of the four factors. To specify the model, simply list the main effects with
the ESTIMATE= option, since these are the effects of interest. Furthermore, if you consider the two-factor interactions to
be significant but are not interested in estimating them, then list these interactions with the NONNEGLIGIBLE= option.
design in order to estimate the main effects of the four factors. To specify the model, simply list the main effects with
the ESTIMATE= option, since these are the effects of interest. Furthermore, if you consider the two-factor interactions to
be significant but are not interested in estimating them, then list these interactions with the NONNEGLIGIBLE= option.
See Example 7.8 for an example that uses the ESTIMATE= option. See Theory of Orthogonal Designs for details about how the FACTEX procedure interprets the model and derives an appropriate confounding scheme.
-
RESOLUTION=r
RESOLUTION=MAXIMUM
-
specifies the resolution of the design. The resolution number r must be a positive integer greater than or equal to 3. The interpretation of r is as follows:
-
If r is odd, then the effects of interest are taken to be those of order 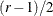 or less.
or less.
-
If r is even, then the effects of interest are taken to be those of order 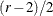 or less, and the nonnegligible effects are taken to be those of order
or less, and the nonnegligible effects are taken to be those of order 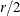 or less.
or less.
If you specify RESOLUTION=MAXIMUM, the FACTEX procedure searches for a design with the highest resolution that satisfies the
SIZE statement requirements.
You can use RES or R for the keyword RESOLUTION and MAX for MAXIMUM.
For more information about design resolution, see the section Resolution. For an example of model specification that uses the RESOLUTION=r option, see the section Example of a Half-Fraction Factorial Design. For an example of the RESOLUTION=MAX option, see the section Example of a Full Factorial Design in Two Blocks.
The following options for the MODEL statement are available:
-
MAXCLEAR <(d)>
-
requests a search for a design that maximizes the number of clear interactions. Clear interactions are those which are not
aliased with any other effects that are either required to be estimable or assumed to be nonnegligible. Specifying (d) immediately after the MAXCLEAR option requests a search for a maximum-clarity design that involves interactions up to order
d. The default value for d is determined automatically from the model, as it is for the ALIASING
option in the EXAMINE statement, as follows:
-
If you specify the model with a resolution number r in the MODEL statement, then d is the integer part of 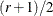 .
.
-
If you specify the model with a list of effects in the MODEL statement, then d is the larger of the following, where main effects have order 1, two-factor interactions have order 2, and so on:
For details about MaxClear designs, see the section MaxClear Designs.
-
MINABS <(d)>
-
requests a search for a design that has minimum aberration. Specifying (d) immediately after the MINABS option requests a search for a minimum aberration design that involves interactions up to order
d. The default value for d is determined automatically from the model as follows:
-
If you specify the model with a resolution number r in the MODEL statement, then 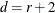 .
.
-
If you specify the model with a list of effects in the MODEL statement, then d is the larger of the following, where main effects have order 1, two-factor interactions have order 2, and so on:
See the section Minimum Aberration for more information. For an example of the MINABS option, see Example 7.11.
Examples of the MODEL Statement
Suppose you specify a design with the following FACTORS statement, where the number of factors f can be replaced with a number:
factors x1-xf;
Then Table 7.6 lists equivalent ways to specify common models.
Table 7.6: Equivalent of Model Specifications
|
RES= option
|
EST= and NONNEG= options
|
|
model res=3
|
model est=(x1-x+f);
|
|
model res=4
|
model est=(x1-x+ f) nonneg=(x1|x2|x3|+…+|x+f+@2);
|
|
model res=5
|
model est=(x1|x2|x3|+…+|x+ f+@2);
|
The resolution specification is more concise than the effects specification and is also more efficient in an algorithmic sense.
To decrease the time required to find a design, particularly for designs with a large number of factors, you should specify
your model that uses the RESOLUTION= option rather than listing the effects. For more on interpreting the resolution number,
see the section Resolution.