Introduction: MACONTROL Procedure
The MACONTROL procedure creates moving average control charts, which are tools for deciding whether a process is in a state of statistical control and for detecting shifts in a process average. The procedure creates the following two types of charts:
-
uniformly weighted moving average charts (commonly referred to as moving average charts). Each point on a moving average chart represents the average of the w most recent subgroup means, including the present subgroup mean. The next moving average is computed by dropping the oldest of the previous w subgroup means and including the newest subgroup mean.
The constant w, often referred to as the span of the moving average, is a parameter of the moving average chart. There is an inverse relationship between w and the magnitude of the shift to be detected; larger values of w are used to guard against smaller shifts.
-
exponentially weighted moving average (EWMA) charts, also referred to as geometric moving average (GMA) charts. Each point on an EWMA chart represents the weighted average of all the previous subgroup means, including the mean of the present subgroup sample. The weights decrease exponentially going backward in time.
The weight r
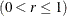 assigned to the present subgroup sample mean is a parameter of the EWMA chart. Small values of r are used to guard against small shifts. If r = 1, the EWMA chart reduces to a Shewhart
assigned to the present subgroup sample mean is a parameter of the EWMA chart. Small values of r are used to guard against small shifts. If r = 1, the EWMA chart reduces to a Shewhart 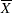 chart.
chart.
In the MACONTROL procedure, the EWMACHART statement produces EWMA charts, and the MACHART statement produces uniformly weighted moving average charts.
In contrast to the Shewhart chart where each point is based on information from a single subgroup sample, each point on a moving average chart combines information from the current sample and past samples. Consequently, the moving average chart is more sensitive to small shifts in the process average. On the other hand, it is more difficult to interpret patterns of points on a moving average chart, since consecutive moving averages can be highly correlated, as pointed out by Nelson (1983).
You can use the MACONTROL procedure to
-
read raw data (actual measurements) or summarized data (subgroup means and standard deviations) to create charts
-
specify control limits as probability limits or in terms of a multiple of the standard error of the moving average
-
adjust the control limits to compensate for unequal subgroup sample sizes
-
accept numeric- or character-valued subgroup variables
-
display subgroups with date and time formats
-
estimate the process standard deviation
 using a variety of methods or specify a standard (known) value for
using a variety of methods or specify a standard (known) value for 
-
analyze multiple process variables in the same chart statement
-
provide multiple chart statements. If used with a BY statement, the procedure generates charts separately for BY groups of observations.
-
tabulate the information displayed in the control chart
-
save moving averages, control limits, and control limit parameters in output data sets
-
superimpose plotted points with stars (polygons) whose vertices indicate the values of multivariate data related to the process
-
display a trend chart below the moving average chart that plots a systematic or fitted trend in the data
-
produce charts as traditional graphics, ODS Graphics output, or legacy line printer charts. Line printer charts can use special formatting characters that improve the appearance of the chart. Traditional graphics can be annotated, saved, and replayed.