| The Unconstrained Nonlinear Programming Solver |
| Conditions of Optimality |
Before beginning the discussion, the following notation is presented for easy reference:

is the dimension of
 (that is, the number of decision variables).
(that is, the number of decision variables). 
is the iteration (that is, the vector of
 decision variables).
decision variables). 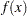
is the objective function.
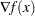
is the gradient of the objective function.
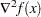
is the Hessian matrix of the objective function.
Denote the feasible region as 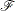 . In unconstrained problems, any point
. In unconstrained problems, any point 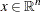 is a feasible point. Therefore, the set
is a feasible point. Therefore, the set 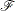 is the entire
is the entire 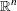 space.
space.
A point  is a local solution of the problem if there exists a neighborhood
is a local solution of the problem if there exists a neighborhood 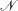 of
of  such that
such that
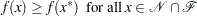 |
Further, a point  is a strict local solution if strict inequality holds in the preceding case; that is,
is a strict local solution if strict inequality holds in the preceding case; that is,
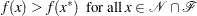 |
A point 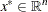 is a global solution of the problem if no point in
is a global solution of the problem if no point in  has a smaller function value than
has a smaller function value than 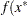 ); that is,
); that is,
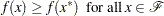 |
All the algorithms in the NLPU solver find a local minimum of an optimization problem.
Unconstrained Optimization
The following conditions hold for unconstrained optimization problems:
First-order necessary conditions: If
 is a local solution and
is a local solution and 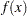 is continuously differentiable in some neighborhood of
is continuously differentiable in some neighborhood of  , then
, then 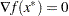
Second-order necessary conditions: If
 is a local solution and
is a local solution and 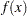 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of  , then
, then 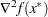 is positive semidefinite.
is positive semidefinite. Second-order sufficient conditions: If
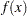 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of  and
and 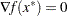 and
and 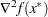 is positive definite, then
is positive definite, then  is a strict local solution.
is a strict local solution.
Copyright © SAS Institute, Inc. All Rights Reserved.