The following example is used in many test libraries for nonlinear programming and was taken originally from Bracken and McCormick (1968).
The problem is to determine the composition of a mixture of various chemicals satisfying its chemical equilibrium state. The second law of thermodynamics implies that a mixture of chemicals satisfies its chemical equilibrium state (at a constant temperature and pressure) when the free energy of the mixture is reduced to a minimum. Therefore the composition of the chemicals satisfying its chemical equilibrium state can be found by minimizing the function of the free energy of the mixture.
Notation:
|
|
number of chemical elements in the mixture |
|
|
number of compounds in the mixture |
|
|
number of moles for compound |
|
|
total number of moles in the mixture |
|
|
number of atoms of element |
|
|
atomic weight of element |
Constraints for the Mixture:
-
The number of moles must be positive:
![\[ x_ j > 0 , \quad j=1,\dots ,n \]](images/ormplpug_nlp0575.png)
-
There are
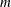 mass balance relationships,
mass balance relationships,
![\[ \sum _{j=1}^ n a_{ij} x_ j = b_ i , \quad i=1,\dots ,m \]](images/ormplpug_nlp0576.png)
Objective Function: Total Free Energy of Mixture
with
where ![]() is the model standard free energy function for the
is the model standard free energy function for the ![]() th compound (found in tables) and
th compound (found in tables) and ![]() is the total pressure in atmospheres.
is the total pressure in atmospheres.
Minimization Problem:
Determine the parameters ![]() that minimize the objective function
that minimize the objective function ![]() subject to the nonnegativity and linear balance constraints.
subject to the nonnegativity and linear balance constraints.
Numeric Example:
Determine the equilibrium composition of compound ![]() at temperature
at temperature ![]() and pressure
and pressure ![]() .
.
|
|
||||||
|
|
|
|
||||
|
|
Compound |
|
|
|
|
|
|
1 |
|
-10.021 |
-6.089 |
1 |
||
|
2 |
|
-21.096 |
-17.164 |
2 |
||
|
3 |
|
-37.986 |
-34.054 |
2 |
1 |
|
|
4 |
|
-9.846 |
-5.914 |
1 |
||
|
5 |
|
-28.653 |
-24.721 |
2 |
||
|
6 |
|
-18.918 |
-14.986 |
1 |
1 |
|
|
7 |
|
-28.032 |
-24.100 |
1 |
1 |
|
|
8 |
|
-14.640 |
-10.708 |
1 |
||
|
9 |
|
-30.594 |
-26.662 |
2 |
||
|
10 |
|
-26.111 |
-22.179 |
1 |
1 |
|
Example Specification:
proc nlp tech=tr pall;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
end;
run;
Displayed Output:
The iteration history given in Output 7.8.1 does not show any problems.
Output 7.8.1: Iteration History
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Trust Region Radius |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 2 | 3 | ' | -47.33412 | 2.2790 | 6.0765 | 2.456 | 1.000 | |
| 2 | 0 | 3 | 3 | ' | -47.70043 | 0.3663 | 8.5592 | 0.908 | 0.418 | |
| 3 | 0 | 4 | 3 | -47.73074 | 0.0303 | 6.4942 | 0 | 0.359 | ||
| 4 | 0 | 5 | 3 | -47.73275 | 0.00201 | 4.7606 | 0 | 0.118 | ||
| 5 | 0 | 6 | 3 | -47.73554 | 0.00279 | 3.2125 | 0 | 0.0168 | ||
| 6 | 0 | 7 | 3 | -47.74223 | 0.00669 | 1.9552 | 110.6 | 0.00271 | ||
| 7 | 0 | 8 | 3 | -47.75048 | 0.00825 | 1.1157 | 102.9 | 0.00563 | ||
| 8 | 0 | 9 | 3 | -47.75876 | 0.00828 | 0.4165 | 3.787 | 0.0116 | ||
| 9 | 0 | 10 | 3 | -47.76101 | 0.00224 | 0.0716 | 0 | 0.0121 | ||
| 10 | 0 | 11 | 3 | -47.76109 | 0.000083 | 0.00238 | 0 | 0.0111 | ||
| 11 | 0 | 12 | 3 | -47.76109 | 9.609E-8 | 2.733E-6 | 0 | 0.00248 |
| Optimization Results | |||
|---|---|---|---|
| Iterations | 11 | Function Calls | 13 |
| Hessian Calls | 12 | Active Constraints | 3 |
| Objective Function | -47.76109086 | Max Abs Gradient Element | 1.8637499E-6 |
| Lambda | 0 | Actual Over Pred Change | 0 |
| Radius | 0.0024776027 | ||
| GCONV convergence criterion satisfied. |
Output 7.8.2 lists the optimal parameters with the gradient.
Output 7.8.2: Optimization Results
| Optimization Results | |||
|---|---|---|---|
| Parameter Estimates | |||
| N | Parameter | Estimate | Gradient Objective Function |
| 1 | x1 | 0.040668 | -9.785055 |
| 2 | x2 | 0.147730 | -19.570110 |
| 3 | x3 | 0.783153 | -34.792170 |
| 4 | x4 | 0.001414 | -12.968921 |
| 5 | x5 | 0.485247 | -25.937841 |
| 6 | x6 | 0.000693 | -22.753976 |
| 7 | x7 | 0.027399 | -28.190984 |
| 8 | x8 | 0.017947 | -15.222060 |
| 9 | x9 | 0.037314 | -30.444120 |
| 10 | x10 | 0.096871 | -25.007115 |
The three equality constraints are satisfied at the solution, as shown in Output 7.8.3.
Output 7.8.3: Linear Constraints at Solution
| Linear Constraints Evaluated at Solution | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACT | -3.608E-16 | = | 2.0000 | - | 1.0000 | * | x1 | - | 2.0000 | * | x2 | - | 2.0000 | * | x3 | - | 1.0000 | * | x6 | - | 1.0000 | * | x10 |
| 2 | ACT | 2.2204E-16 | = | 1.0000 | - | 1.0000 | * | x4 | - | 2.0000 | * | x5 | - | 1.0000 | * | x6 | - | 1.0000 | * | x7 | ||||
| 3 | ACT | -1.943E-16 | = | 1.0000 | - | 1.0000 | * | x3 | - | 1.0000 | * | x7 | - | 1.0000 | * | x8 | - | 2.0000 | * | x9 | - | 1.0000 | * | x10 |
The Lagrange multipliers are given in Output 7.8.4.
Output 7.8.4: Lagrange Multipliers
| First Order Lagrange Multipliers | ||
|---|---|---|
| Active Constraint | Lagrange Multiplier |
|
| Linear EC | [1] | 9.785055 |
| Linear EC | [2] | 12.968921 |
| Linear EC | [3] | 15.222060 |
The elements of the projected gradient must be small to satisfy a necessary first-order optimality condition. The projected gradient is given in Output 7.8.5.
Output 7.8.5: Projected Gradient
| Projected Gradient | |
|---|---|
| Free Dimension |
Projected Gradient |
| 1 | 4.5770108E-9 |
| 2 | 6.868355E-10 |
| 3 | -7.283013E-9 |
| 4 | -0.000001864 |
| 5 | -0.000001434 |
| 6 | -0.000001361 |
| 7 | -0.000000294 |
The projected Hessian matrix shown in Output 7.8.6 is positive definite, satisfying the second-order optimality condition.
Output 7.8.6: Projected Hessian Matrix
| Projected Hessian Matrix | |||||||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| X1 | 20.903196985 | -0.122067474 | 2.6480263467 | 3.3439156526 | -1.373829641 | -1.491808185 | 1.1462413516 |
| X2 | -0.122067474 | 565.97299938 | 106.54631863 | -83.7084843 | -37.43971036 | -36.20703737 | -16.635529 |
| X3 | 2.6480263467 | 106.54631863 | 1052.3567179 | -115.230587 | 182.89278895 | 175.97949593 | -57.04158208 |
| X4 | 3.3439156526 | -83.7084843 | -115.230587 | 37.529977667 | -4.621642366 | -4.574152161 | 10.306551561 |
| X5 | -1.373829641 | -37.43971036 | 182.89278895 | -4.621642366 | 79.326057844 | 22.960487404 | -12.69831637 |
| X6 | -1.491808185 | -36.20703737 | 175.97949593 | -4.574152161 | 22.960487404 | 66.669897023 | -8.121228758 |
| X7 | 1.1462413516 | -16.635529 | -57.04158208 | 10.306551561 | -12.69831637 | -8.121228758 | 14.690478023 |
The following PROC NLP call uses a specified analytical gradient and the Hessian matrix is computed by finite-difference approximations based on the analytic gradient:
proc nlp tech=tr fdhessian all;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
array g[10] g1-g10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
g[j] = c[j] + log(x[j] / s);
end;
run;
The results are almost identical to those of the previous run.