PROC INTPOINT is designed so that there are as few rules as possible that you must obey when inputting a problem’s data. Raw data are acceptable. This should cut the amount of processing required to groom the data before it is input to PROC INTPOINT. Data formats are so flexible that, due to space restrictions, all possible forms for a problem’s data are not shown here. Try any reasonable form for your problem’s data; it should be acceptable. PROC INTPOINT will outline its objections.
You can supply the same piece of data several ways. You do not have to restrict yourself to using any particular one. If you use several ways, PROC INTPOINT checks that the data are consistent each time that the data are encountered. After all input data sets have been read, data are merged so that the problem is described completely. The observations can be in any order.
See the section Getting Started: NPSC Problems and the section Introductory NPSC Example for a description of this input data set.
Note: Information for an arc or nonarc variable can be specified in more than one observation. For example, consider an arc directed from node A toward node B that has a cost of 50, capacity of 100, and lower flow bound of 10 flow units. Some possible observations in the ARCDATA= data set are as follows:
_tail_ _head_ _cost_ _capac_ _lo_
A B 50 . .
A B . 100 .
A B . . 10
A B 50 100 .
A B . 100 10
A B 50 . 10
A B 50 100 10
Similarly, for a nonarc variable that has an upper bound of 100, a lower bound of 10, and an objective function coefficient
of 50, the _TAIL_ and _HEAD_ values are missing.
When solving an LP that has an LP variable named my_var with an upper bound of 100, a lower bound of 10, and an objective function coefficient of 50, some possible observations
in the ARCDATA= data set are
_name_ _cost_ _capac_ _lo_ my_var 50 . . my_var . 100 . my_var . . 10 my_var 50 100 . my_var . 100 10 my_var 50 . 10 my_var 50 100 10
Regardless of whether the data in the CONDATA= data set is in the sparse or dense format, you will receive a warning if PROC INTPOINT finds a constraint row that has no coefficients. You will also be warned if any nonarc or LP variable has no constraint coefficients.
If the dense format is used, most SAS variables in the CONDATA= data set belong to the VAR list. The names of the SAS variables belonging to this list have names of arc and nonarc variables or, if solving an LP, names of the LP variables. These names can be values of the SAS variables in the ARCDATA= data set that belong to the NAME list, or names of nonarc variables, or names in the form tail_head, or any combination of these three forms. Names in the form tail_head are default arc names, and if you use them, you must specify node names in the ARCDATA= data set (values of the TAILNODE and HEADNODE list variables).
The CONDATA= data set can have three other SAS variables belonging, respectively, to the ROW, the TYPE, and the RHS lists. The CONDATA= data set of the oil industry example in the section Introductory NPSC Example uses the dense data format.
Consider the SAS code that creates a dense format CONDATA= data set that has data for three constraints. This data set was used in the section Introductory NPSC Example.
data cond1;
input m_e_ref1 m_e_ref2 thruput1 r1_gas thruput2 r2_gas
_type_ $ _rhs_;
datalines;
-2 . 1 . . . >= -15
. -2 . . 1 . GE -15
. . -3 4 . . EQ 0
. . . . -3 4 = 0
;
You can use nonconstraint type values to furnish data on costs, capacities, lower flow bounds (and, if there are nonarc or LP variables, objective function coefficients and upper and lower bounds). You need not have such (or as much) data in the ARCDATA= data set. The first three observations in the following data set are examples of observations that provide cost, capacity, and lower bound data.
data cond1b;
input m_e_ref1 m_e_ref2 thruput1 r1_gas thruput2 r2_gas
_type_ $ _rhs_;
datalines;
63 81 200 . 220 . cost .
95 80 175 140 100 100 capac .
20 10 50 . 35 . lo .
-2 . 1 . . . >= -15
. -2 . . 1 . GE -15
. . -3 4 . . EQ 0
. . . . -3 4 = 0
;
If a ROW list variable is used, the data for a constraint can be spread over more than one observation. To illustrate, the data for
the first constraint (which is called con1) and the cost and capacity data (in special rows called costrow and caprow, respectively) are spread over more than one observation in the following data set.
data cond1c;
input _row_ $
m_e_ref1 m_e_ref2 thruput1 r1_gas thruput2 r2_gas
_type_ $ _rhs_;
datalines;
costrow 63 . . . . . . .
costrow . 81 200 . . . cost .
. . . . . 220 . cost .
caprow . . . . . . capac .
caprow 95 . 175 . 100 100 . .
caprow . 80 175 140 . . . .
lorow 20 10 50 . 35 . lo .
con1 -2 . 1 . . . . .
con1 . . . . . . >= -15
con2 . -2 . . 1 . GE -15
con3 . . -3 4 . . EQ 0
con4 . . . . -3 4 = 0
;
Using both ROW and TYPE lists, you can use special row names. Examples of these are costrow and caprow in the last data set. It should be restated that in any of the input data sets of PROC INTPOINT, the order of the observations
does not matter. However, the CONDATA= data set can be read more quickly if PROC INTPOINT knows what type of constraint or special row a ROW list variable value is. For example, when the first observation is read, PROC INTPOINT does not know whether costrow is a constraint or special row and how to interpret the value 63 for the arc with the name m_e_ref1. When PROC INTPOINT reads the second observation, it learns that costrow has cost type and that the values 81 and 200 are costs. When the entire CONDATA= data set has been read, PROC INTPOINT knows the type of all special rows and constraints. Data that PROC INTPOINT had to
set aside (such as the first observation 63 value and the costrow ROW list variable value, which at the time had unknown type, but is subsequently known to be a cost special row) is reprocessed.
During this second pass, if a ROW list variable value has unassigned constraint or special row type, it is treated as a constraint with DEFCONTYPE= (or DEFCONTYPE= default) type. Associated VAR list variable values are coefficients of that constraint.
The side constraints usually become sparse as the problem size increases. When the sparse data format of the CONDATA= data set is used, only nonzero constraint coefficients must be specified. Remember to specify the SPARSECONDATA option in the PROC INTPOINT statement. With the sparse method of specifying constraint information, the names of arc and nonarc variables or, if solving an LP, the names of LP variables do not have to be valid SAS variable names.
A sparse format CONDATA= data set for the oil industry example in the section Introductory NPSC Example is displayed below.
title 'Setting Up Condata = Cond2 for PROC INTPOINT'; data cond2; input _column_ $ _row1 $ _coef1 _row2 $ _coef2 ; datalines; m_e_ref1 con1 -2 . . m_e_ref2 con2 -2 . . thruput1 con1 1 con3 -3 r1_gas . . con3 4 thruput2 con2 1 con4 -3 r2_gas . . con4 4 _type_ con1 1 con2 1 _type_ con3 0 con4 0 _rhs_ con1 -15 con2 -15 ;
Recall that the COLUMN list variable values _type_ and _rhs_ are the default values of the TYPEOBS= and RHSOBS= options. Also, the default rhs value of constraints (con3 and con4) is zero. The third to last observation has the value _type_ for the COLUMN list variable. The _ROW1 variable value is con1, and the _COEF1_ variable has the value 1. This indicates that the constraint con1 is greater than or equal to type (because the value 1 is greater than zero). Similarly, the data in the second to last observation’s _ROW2 and _COEF2 variables indicate that con2 is an equality constraint (0 equals zero).
An alternative, using a TYPE list variable, is
title 'Setting Up Condata = Cond3 for PROC INTPOINT'; data cond3; input _column_ $ _row1 $ _coef1 _row2 $ _coef2 _type_ $ ; datalines; m_e_ref1 con1 -2 . . >= m_e_ref2 con2 -2 . . . thruput1 con1 1 con3 -3 . r1_gas . . con3 4 . thruput2 con2 1 con4 -3 . r2_gas . . con4 4 . . con3 . con4 . eq . con1 -15 con2 -15 ge ;
If the COLUMN list variable is missing in a particular observation (the last 2 observations in the data set cond3, for instance), the constraints named in the ROW list variables all have the constraint type indicated by the value in the TYPE list variable. It is for this type of observation that you are allowed more ROW list variables than COEF list variables. If corresponding COEF list variables are not missing (for example, the last observation in the data set cond3), these values are the rhs values of those constraints. Therefore, you can specify both constraint type and rhs in the same
observation.
As in the previous CONDATA= data set, if the COLUMN list variable is an arc or nonarc variable, the COEF list variable values are coefficient values for that arc or nonarc variable in the constraints indicated in the corresponding
ROW list variables. If in this same observation the TYPE list variable contains a constraint type, all constraints named in the ROW list variables in that observation have this constraint type (for example, the first observation in the data set cond3). Therefore, you can specify both constraint type and coefficient information in the same observation.
Also note that DEFCONTYPE=EQ could have been specified, saving you from having to include in the data that con3 and con4 are of this type.
In the oil industry example, arc costs, capacities, and lower flow bounds are presented in the ARCDATA= data set. Alternatively, you could have used the following input data sets. The arcd2 data set has only two SAS variables. For each arc, there is an observation in which the arc’s tail and head node are specified.
title3 'Setting Up Arcdata = Arcd2 for PROC INTPOINT'; data arcd2; input _from_&$11. _to_&$15. ; datalines; middle east refinery 1 middle east refinery 2 u.s.a. refinery 1 u.s.a. refinery 2 refinery 1 r1 refinery 2 r2 r1 ref1 gas r1 ref1 diesel r2 ref2 gas r2 ref2 diesel ref1 gas servstn1 gas ref1 gas servstn2 gas ref1 diesel servstn1 diesel ref1 diesel servstn2 diesel ref2 gas servstn1 gas ref2 gas servstn2 gas ref2 diesel servstn1 diesel ref2 diesel servstn2 diesel ;
title 'Setting Up Condata = Cond4 for PROC INTPOINT'; data cond4; input _column_&$27. _row1 $ _coef1 _row2 $ _coef2 _type_ $ ; datalines; . con1 -15 con2 -15 ge . costrow . . . cost . . . caprow . capac middle east_refinery 1 con1 -2 . . . middle east_refinery 2 con2 -2 . . . refinery 1_r1 con1 1 con3 -3 . r1_ref1 gas . . con3 4 = refinery 2_r2 con2 1 con4 -3 . r2_ref2 gas . . con4 4 eq middle east_refinery 1 costrow 63 caprow 95 . middle east_refinery 2 costrow 81 caprow 80 . u.s.a._refinery 1 costrow 55 . . . u.s.a._refinery 2 costrow 49 . . . refinery 1_r1 costrow 200 caprow 175 . refinery 2_r2 costrow 220 caprow 100 . r1_ref1 gas . . caprow 140 . r1_ref1 diesel . . caprow 75 . r2_ref2 gas . . caprow 100 . r2_ref2 diesel . . caprow 75 . ref1 gas_servstn1 gas costrow 15 caprow 70 . ref1 gas_servstn2 gas costrow 22 caprow 60 . ref1 diesel_servstn1 diesel costrow 18 . . . ref1 diesel_servstn2 diesel costrow 17 . . . ref2 gas_servstn1 gas costrow 17 caprow 35 . ref2 gas_servstn2 gas costrow 31 . . . ref2 diesel_servstn1 diesel costrow 36 . . . ref2 diesel_servstn2 diesel costrow 23 . . . middle east_refinery 1 . 20 . . lo middle east_refinery 2 . 10 . . lo refinery 1_r1 . 50 . . lo refinery 2_r2 . 35 . . lo ref2 gas_servstn1 gas . 5 . . lo ;
The first observation in the cond4 data set defines con1 and con2 as greater than or equal to (![]() ) constraints that both (by coincidence) have rhs values of -15. The second observation defines the special row
) constraints that both (by coincidence) have rhs values of -15. The second observation defines the special row costrow as a cost row. When costrow is a ROW list variable value, the associated COEF list variable value is interpreted as a cost or objective function coefficient. PROC INTPOINT has to do less work if constraint
names and special rows are defined in observations near the top of a data set, but this is not a strict requirement. The fourth
to ninth observations contain constraint coefficient data. Observations seven and nine have TYPE list variable values that indicate that constraints con3 and con4 are equality constraints. The last five observations contain lower flow bound data. Observations that have an arc or nonarc
variable name in the COLUMN list variable, a nonconstraint type TYPE list variable value, and a value in (one of) the COEF list variables are valid.
The following data set is equivalent to the cond4 data set.
title 'Setting Up Condata = Cond5 for PROC INTPOINT';
data cond5;
input _column_&$27. _row1 $ _coef1 _row2 $ _coef2 _type_ $ ;
datalines;
middle east_refinery 1 con1 -2 costrow 63 .
middle east_refinery 2 con2 -2 lorow 10 .
refinery 1_r1 . . con3 -3 =
r1_ref1 gas caprow 140 con3 4 .
refinery 2_r2 con2 1 con4 -3 .
r2_ref2 gas . . con4 4 eq
. CON1 -15 CON2 -15 GE
ref2 diesel_servstn1 diesel . 36 costrow . cost
. . . caprow . capac
. lorow . . . lo
middle east_refinery 1 caprow 95 lorow 20 .
middle east_refinery 2 caprow 80 costrow 81 .
u.s.a._refinery 1 . . . 55 cost
u.s.a._refinery 2 costrow 49 . . .
refinery 1_r1 con1 1 caprow 175 .
refinery 1_r1 lorow 50 costrow 200 .
refinery 2_r2 costrow 220 caprow 100 .
refinery 2_r2 . 35 . . lo
r1_ref1 diesel caprow2 75 . . capac
r2_ref2 gas . . caprow 100 .
r2_ref2 diesel caprow2 75 . . .
ref1 gas_servstn1 gas costrow 15 caprow 70 .
ref1 gas_servstn2 gas caprow2 60 costrow 22 .
ref1 diesel_servstn1 diesel . . costrow 18 .
ref1 diesel_servstn2 diesel costrow 17 . . .
ref2 gas_servstn1 gas costrow 17 lorow 5 .
ref2 gas_servstn1 gas . . caprow2 35 .
ref2 gas_servstn2 gas . 31 . . cost
ref2 diesel_servstn2 diesel . . costrow 23 .
;
Converting from an NPSC to an LP Problem
If you have data for a linear programming program that has an embedded network, the steps required to change that data into a form that is acceptable by PROC INTPOINT are
-
Identify the nodal flow conservation constraints. The coefficient matrix of these constraints (a submatrix of the LP’s constraint coefficient matrix) has only two nonzero elements in each column, -1 and 1.
-
Assign a node to each nodal flow conservation constraint.
-
The rhs values of conservation constraints are the corresponding node’s supplies and demands. Use this information to create the NODEDATA= data set.
-
Assign an arc to each column of the flow conservation constraint coefficient matrix. The arc is directed from the node associated with the row that has the
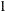 element in it and directed toward to the node associated with the row that has the
element in it and directed toward to the node associated with the row that has the 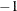 element in it. Set up the ARCDATA= data set that has two SAS variables. This data set could resemble ARCDATA=arcd2. These will eventually be the TAILNODE and HEADNODE list variables when PROC INTPOINT is used. Each observation consists of the tail and head node of each arc.
element in it. Set up the ARCDATA= data set that has two SAS variables. This data set could resemble ARCDATA=arcd2. These will eventually be the TAILNODE and HEADNODE list variables when PROC INTPOINT is used. Each observation consists of the tail and head node of each arc.
-
Remove from the data of the linear program all data concerning the nodal flow conservation constraints.
-
Put the remaining data into a CONDATA= data set. This data set will probably resemble CONDATA=cond4 or CONDATA=cond5.
The following list illustrates possible CONDATA= data set observation sparse formats. a1, b1, b2, b3 and c1 have as a _COLUMN_ variable value either the name of an arc (possibly in the form tail_head) or the name of a nonarc variable (if you are solving an NPSC), or the name of the LP variable (if you are solving an LP).
These are collectively referred to as variable in the tables that follow.
-
If there is no TYPE list variable in the CONDATA= data set, the problem must be constrained and there is no nonconstraint data in the CONDATA= data set:
_COLUMN_ _ROWx_ _COEFx_ _ROWy_ (no _COEFy_) (may not be in CONDATA) a1 variable constraint lhs coef +------------+ a2 _TYPE_ or constraint -1 0 1 | | TYPEOBS= | | a3 _RHS_ or constraint rhs value | constraint | RHSOBS= or | or | missing | missing | a4 _TYPE_ or constraint missing | | TYPEOBS= | | a5 _RHS_ or constraint missing | | RHSOBS= or +------------+ missingObservations of the form a4 and a5 serve no useful purpose but are still allowed to make problem generation easier.
-
If there are no ROW list variables in the data set, the problem has no constraints and the information is nonconstraint data. There must be a TYPE list variable and only one COEF list variable in this case. The COLUMN list variable has as values the names of arcs or nonarc variables and must not have missing values or special row names as values:
_COLUMN_ _TYPE_ _COEFx_ b1 variable UPPERBD capacity b2 variable LOWERBD lower flow b3 variable COST cost -
Using a TYPE list variable for constraint data implies the following:
_COLUMN_ _TYPE_ _ROWx_ _COEFx_ _ROWy_ (no _COEFy_) (may not be in CONDATA) c1 variable missing +-----+ lhs coef +------------+ c2 _TYPE_ or missing | c | -1 0 1 | | TYPEOBS= | o | | | c3 _RHS_ or missing | n | rhs value | constraint | missing | s | | or | or RHSOBS= | t | | missing | c4 variable con type | r | lhs coef | | c5 _RHS_ or con type | a | rhs value | | missing | i | | | or RHSOBS= | n | | | c6 missing TYPE | t | -1 0 1 | | c7 missing RHS +-----+ rhs value +------------+If the observation is in form c4 or c5, and the
_COEFx_values are missing, the constraint is assigned the type data specified in the_TYPE_variable. -
Using a TYPE list variable for arc and nonarc variable data implies the following:
_COLUMN_ _TYPE_ _ROWx_ _COEFx_ _ROWy_ (no _COEFy_) (may not be in CONDATA) +---------+ +---------+ +---------+ d1 variable | UPPERBD | | missing | capacity | missing | d2 variable | LOWERBD | | or | lowerflow | or | d3 variable | COST | | special | cost | special | | | | row | | row | | | | name | | name | | | +---------+ | | d4 missing | | | special | | | | | | row | | | +---------+ | name | +---------+ d5 variable missing | | value that missing | |is interpreted | |according to +---------+ _ROWx_The observations of the form d1 to d5 can have ROW list variable values. Observation d4 must have ROW list variable values. The ROW value is put into the ROW name tree so that when dealing with observation d4 or d5, the COEF list variable value is interpreted according to the type of ROW list variable value. For example, the following three observations define the
_ROWx_variable values up_row, lo_row, and co_row as being an upper value bound row, lower value bound row, and cost row, respectively:_COLUMN_ _TYPE_ _ROWx_ _COEFx_ . UPPERBD up_row . variable_a LOWERBD lo_row lower flow variable_b COST co_row costPROC INTPOINT is now able to correctly interpret the following observation:
_COLUMN_ _TYPE_ _ROW1_ _COEF1_ _ROW2_ _COEF2_ _ROW3_ _COEF3_ var_c . up_row upval lo_row loval co_row costIf the TYPE list variable value is a constraint type and the value of the COLUMN list variable equals the value of the TYPEOBS= option or the default value
_TYPE_, the TYPE list variable value is ignored.
See the section Getting Started: NPSC Problems and the section Introductory NPSC Example for a description of this input data set.