Language Reference
CALL SEQ (prob, domain <*>, TSCALE=tscale <*>, EPS=eps <*>, DEN=den );
CALL SEQSCALE (prob, gscale, domain, level <*>, IGUESS=iguess <*>, TSCALE=tscale <*>, EPS=eps <*>, DEN=den );
CALL SEQSHIFT (prob, shift, domain, plevel <*>, IGUESS=iguess <*>, TSCALE=tscale <*>, EPS=eps <*>, DEN=den );
The SEQ, SEQSCALE, and SEQSHIFT subroutines perform discrete sequential tests.
The SEQSHIFT subroutine returns the following values:
- prob
-
is an
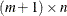 matrix. The
matrix. The ![$[i,j]$](images/imlug_langref1292.png) entry in the array contains the probability at the
entry in the array contains the probability at the ![$[i,j]$](images/imlug_langref1292.png) entry of the argument domain. Also, the probability at infinity at every level j is returned in the last entry (
entry of the argument domain. Also, the probability at infinity at every level j is returned in the last entry (![$[m+1,j]$](images/imlug_langref1293.png) ) of column j. Upon a successful completion of any routine, this variable is always returned.
) of column j. Upon a successful completion of any routine, this variable is always returned.
- gscale
-
is a numeric variable that returns from the routine SEQSCALE and contains the scaling of the current geometry defined by domain that would yield a given significance level level.
- shift
-
is a numeric variable that returns from the routine SEQSHIFT and contains the shift of current geometry defined by domain that would yield a given power level plevel.
The input arguments to the SEQSHIFT subroutine are as follows:
- domain
-
specifies an
 matrix that contains the boundary points separating the intervals of continuation/stopping of the sequential test. Each column
k contains the boundary points at level k sorted in an ascending order. The values
matrix that contains the boundary points separating the intervals of continuation/stopping of the sequential test. Each column
k contains the boundary points at level k sorted in an ascending order. The values .Mand.Prepresent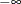 and
and 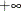 , respectively. They must start on the first row, and any remaining entries must be filled with a missing value. Elements
that follow the missing value in any column are ignored. The number of columns n is equal to the number of stages present in the sequential test. The row dimension m must be even, and it is equal to the maximum number of boundary points in a level. In fact, domain is the tabular form of the finite boundary points. Entries in domain with absolute values that exceed a standardized value of 8 at any level are internally reset to a standardized value of 8
or
, respectively. They must start on the first row, and any remaining entries must be filled with a missing value. Elements
that follow the missing value in any column are ignored. The number of columns n is equal to the number of stages present in the sequential test. The row dimension m must be even, and it is equal to the maximum number of boundary points in a level. In fact, domain is the tabular form of the finite boundary points. Entries in domain with absolute values that exceed a standardized value of 8 at any level are internally reset to a standardized value of 8
or 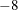 , depending on the sign of the entry. This is reflected in the results returned for the probabilities and the densities.
, depending on the sign of the entry. This is reflected in the results returned for the probabilities and the densities.
- tscale
-
specifies an optional
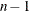 vector that describes the time intervals between two consecutive stages. In the absence of tscale, these time intervals are internally set to 1. The keyword for tscale is TSCALE.
vector that describes the time intervals between two consecutive stages. In the absence of tscale, these time intervals are internally set to 1. The keyword for tscale is TSCALE.
- eps
-
specifies an optional numeric parameter for controlling the absolute precision of the computation. In the absence of eps, the precision is internally set to 1E
 7. The keyword for eps is EPS.
7. The keyword for eps is EPS.
- den
-
specifies an optional character string to describe the name of an
 matrix. The
matrix. The ![$[i,j]$](images/imlug_langref1292.png) entry in the matrix returns the density of the distribution at the
entry in the matrix returns the density of the distribution at the ![$[i,j]$](images/imlug_langref1292.png) entry of the matrix specified by the domain argument. The keyword for den is DEN.
entry of the matrix specified by the domain argument. The keyword for den is DEN.
- iguess
-
specifies an optional numeric parameter that contains an initial guess for the variable gscale in the SEQSCALE subroutine or for the variable mean in the SEQSHIFT subroutine. In general, very good estimates for these initial guesses can be provided by an iterative process, and these estimates become extremely valuable near convergence. The keyword for iguess is IGUESS.
- level
-
specifies a numeric parameter in the SEQSCALE subroutine that contains the required significance level to be achieved through scaling the domain (see the description of SEQSCALE).
- plevel
-
specifies a numeric parameter in the SEQSHIFT subroutine that provides the required power level to be achieved through shifting the domain (see the description of SEQSHIFT).
To compute the probability from a sequential test, you must specify a matrix that contains the boundaries. With the optional
additional information concerning the time intervals and the target accuracy, or their default values, the SEQ subroutine
returns the matrix that contains the probability and optionally returns the density from a sequential test evaluated at each
given point of the boundary. Let ![]() denote the continuation set at each level j.
denote the continuation set at each level j. ![]() is defined to be the union at the jth level of all the intervals bounded from below by the points with even indices
is defined to be the union at the jth level of all the intervals bounded from below by the points with even indices ![]() and from above by the points with odd indices
and from above by the points with odd indices ![]() .
.
The SEQ subroutine computes, with ![]() , the densities
, the densities
with
and
with the associated probability at any point a at level j to be
with
The notation ![]() denotes the vector of time intervals
denotes the vector of time intervals ![]() , and
, and ![]() denotes the probability of continuation at the jth level for a given domain g, a given mean
denotes the probability of continuation at the jth level for a given domain g, a given mean ![]() , and a given time vector
, and a given time vector ![]() . The variance at the
. The variance at the ![]() level can be computed from
level can be computed from ![]() .
.
It is important to understand the limitations that are imposed internally on the domain by the numerical method. Any element
![]() will always be limited within a symmetric interval with standardized values not to exceed 8. That is,
will always be limited within a symmetric interval with standardized values not to exceed 8. That is,
Given a domain g, an optional time vector ![]() , and a probability level
, and a probability level ![]() , the SEQSCALE subroutine finds the amount of scaling s that would solve the problem
, the SEQSCALE subroutine finds the amount of scaling s that would solve the problem
The result for the amount of scaling s is returned as the second argument of the SEQSCALE subroutine, scale. Note that because of the complexity of the problem, the SEQSCALE subroutine will not attempt to scale a domain with multiple intervals of continuation.
For a significance level of ![]() , set
, set ![]() .
.
Given a geometry g, an optional time vector ![]() , and a power level
, and a power level ![]() , the SEQSHIFT subroutine finds the mean
, the SEQSHIFT subroutine finds the mean ![]() that solves
that solves ![]() .
.
Actually, a simple transformation of the variables in the sequential problem yields the following result:
where ![]() is given by
is given by ![]() .
.
Many options are available with the NLP family of optimization routines, which are described in Chapter 4, "Nonlinear Optimization Subroutines."
Consider the following continuation intervals:
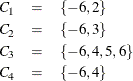
The following statements computes the probability from the sequential test at each boundary point specified in the geometry.
/* function to insert a into the kth column of m */
start table(m,a,k);
if ncol(m) = 0 then m = j(nrow(a),k,.);
if nrow(m) < nrow(a) then m = m// j(nrow(a)-nrow(m),ncol(m),.);
if ncol(m) < k then m = m || j(nrow(m),k-ncol(m),.);
m[1:nrow(a),k] = a;
finish;
call table(m, {-6,2}, 1);
call table(m, {-6,3}, 2);
call table(m, {-6,4,5,6}, 3);
call table(m, {-6,4}, 4);
call seq(prob,m) eps = 1.e-8 den="density";
print m, prob, density;
Figure 24.358 displays the values returned for m, prob and den, respectively.
The probability at the level ![]() at the point
at the point ![]() is prob
is prob![]() , while the density at the same point is density
, while the density at the same point is density![]() .
.
Consider the continuation intervals
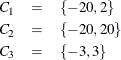
Note that the continuation at level 2 can be effectively considered infinite, and it does not numerically affect the results of the computation at level 3. The following statements verify this by using the tscale parameter to compute this problem.
free m;
call table(m, {-20,2}, 1);
call table(m, {-20,20}, 2);
call table(m, {-3, 3}, 3);
/**************************************/
/* TSCALE has the default value of 1 */
/**************************************/
call seq(prob1,m) eps = 1.e-8 den="density";
print m[format=f5.] prob1[format=e12.5];
call table(mm,{-20,2},1);
call table(mm,{-3,3},2);
/* You can use a 2-step separation between the levels */
/* while dropping the intermediate level at 2 */
tscale = { 2 };
call seq(prob2,mm) eps = 1.e-8 den="density" TSCALE=tscale;
print mm[format=f5.] prob2[format=e12.5];
Figure 24.359 shows the values returned for the variables m, prob1, mm and prob2.
Some internal limitations are imposed on the geometry. Consider the three-level case with geometry m in the preceding statements. Since the tscale variable is not specified, it is set to its default value, ![]() . The variance at the jth level is
. The variance at the jth level is ![]() for
for ![]() . The first level has a lower boundary point of
. The first level has a lower boundary point of ![]() , as represented by the value of
, as represented by the value of ![]() . Since the absolute standardized value is larger than 8, this point is replaced internally by the value
. Since the absolute standardized value is larger than 8, this point is replaced internally by the value ![]() . Hence, the densities and the probabilities reported for the first level at this point are not for the given value
. Hence, the densities and the probabilities reported for the first level at this point are not for the given value ![]() ; instead, they are for the internal value of
; instead, they are for the internal value of ![]() . For practical purposes, this limitation is not severe since the absolute error introduced is of the order of
. For practical purposes, this limitation is not severe since the absolute error introduced is of the order of ![]() .
.
The computations performed by the first call of the SEQ subroutine can be simplified since the second level is large enough to be considered infinite. The matrix MM contains the first and third columns of the matrix M. However, in order to specify the two-step separation between the levels, you must specify tscale=2.
This example verifies some of the results published in Table 3 of Pocock (1982). That is, the following statements verify for the given domain that the significance level is 0.05 and that the power is
![]() under the alternative hypothesis:
under the alternative hypothesis:
proc iml;
/* check whether the numbers yield 0.95 for the alpha level */
bm ={-3.663 -2.884 -2.573 -2.375 -2.037,
-2.988 -2.537 -2.407 -2.346 -2.156,
-2.598 -2.390 -2.390 -2.390 -2.310,
-2.446 -2.404 -2.404 -2.404 -2.396};
bplevel = { 0.5 0.25 0.1 0.05};
level = 0.95; /* this the required alpha value */
sigma = diag(sqrt(1:5)); /* global sigma matrix */
do i = 1 to 4;
m = bm[i,];
plevel = bplevel[i];
geom = (m//(-m))*sigma;
/* Try the null hypothesis */
call seq(prob,geom) eps = 1.e-10;
palpha = (prob[2,]-prob[1,])[5];
/* Try the alternative hypothesis */
call seqshift(prob,mean,geom,plevel);
beta = (prob[2,] -prob[1,])[5];
p = prob[3,]-prob[2,]+prob[1,];
/* Number of patients per group */
tn = 4*mean##2;
maxn = 5*tn;
/* compute the average sample number */
asn = tn *( 5 - (4:0) * p`);
summary = summary // ( palpha || level || beta ||
plevel || tn || maxn ||asn);
end;
print summary[format=10.5];
Notice that the variables eps and tscale have been internally set to their default values. Figure 24.360 shows the computed values, which compare well with the values shown in Table 3 of Pocock (1982). Differences are of the order of ![]() .
.
This example shows how to verify the results in Table 1 of Wang and Tsiatis (1987). For a given ![]() , the following program finds
, the following program finds ![]() that yields a symmetric continuation interval given by
that yields a symmetric continuation interval given by
with a given significance level of ![]() :
:
proc iml;
start func(delta,k) global(level);
m = ((1:k))##delta;
mm = (-m//m);
/* meet the significance level by scaling */
call seqscale(prob,scale,mm,level);
return(scale);
finish;
/* alpha levels of 0.05 and 0.01 */
blevel = {0.95 0.99};
do i = 1 to 2;
level = blevel[i];
free summary;
do delta = 0 to .7 by .1;
free row;
do k=2 to 5;
x = func(delta,k);
row = row || x;
end;
summary = summary //row;
end;
print summary[format=10.5];
end;
Figure 24.361 shows the value of SUMMARY for the 0.95 and 0.99 levels. Notice that since eps and tscale are not specified, they are internally set to their default values.
This example verifies the results in Table 2 of Pocock (1977). The following program finds ![]() that yields a symmetric continuation interval given by
that yields a symmetric continuation interval given by
for five groups. The overall significance level is ![]() (the probability
(the probability ![]() ), and the power is
), and the power is ![]() .
.
%let nl = 5;
proc iml;
start func(plevel) global(level,scale,mean,palpha,beta,tn,asn);
m = sqrt((1: &nl));
mm = -m //m;
/* meet the significance level by scaling */
call seqscale(prob,scale,mm,level);
palpha = (prob[2,]-prob[1,])[&nl];
mm = mm *scale;
/* meet the power condition */
call seqshift(prob,mean,mm,plevel);
return(mean);
finish;
/* alpha = 0.95 */
level = 0.95;
bplevel = { 0.5 .25 .1 0.05 0.01};
free summary;
do i = 1 to 5;
summary = summary || func(bplevel[i]);
end;
print summary[format=10.5];
Figure 24.362 shows the results, which agree with Table 2 of Pocock (1977).
This example illustrates how to find the optimal boundary of the ![]() -class of Wang and Tsiatis (1987). The
-class of Wang and Tsiatis (1987). The ![]() -class boundary has the form
-class boundary has the form
The ![]() -class boundary is optimal if it minimizes the average sample number while satisfying the required significance level
-class boundary is optimal if it minimizes the average sample number while satisfying the required significance level ![]() and the required power
and the required power ![]() . You can use the following program to verify some of the results published in Table 2 and Table 3 of Wang and Tsiatis (1987):
. You can use the following program to verify some of the results published in Table 2 and Table 3 of Wang and Tsiatis (1987):
%let nl = 5;
proc iml;
start func(delta) global(level,plevel,mean,
scale,alpha,beta,tn,asn);
m = ((1: &nl))##delta;
mm = (-m//m);
/* meet the significance level */
call seqscale(prob,scale,mm,level);
alpha = (prob[2,]-prob[1,])[&nl];
mm = mm *scale;
/* meet the power condition */
call seqshift(prob,mean,mm,plevel);
beta = (prob[2,]-prob[1,])[&nl];
/* compute the average sample number */
p = prob[3,]-prob[2,]+prob[1];
tn = 4*mean##2; /* number per group */
asn = tn *( &nl - p *((&nl-1):0)`);
return(asn);
finish;
/* set up the global variables needed by func */
level = 0.95;
plevel = 0.01;
/* set up options used to control the optimization routine */
opt = {0 1 0 1 6};
tc = repeat(.,1,12);
tc[1] = 100;
tc[7] = 1.e-4;
par = { 1.e-13 . 1.e-10 . . .} || . || epsd;
/* provide the initial guess and call nlpdd */
delta = 0.5;
ods select IterStop ConvergenceStatus;
call nlpdd(rc,rx,"func",delta) opt=opt tc=tc par=par;
Figure 24.363 displays the results. The optimal function value of 34.88 agrees with the entry in Table 2 of Wang and Tsiatis (1987) for five groups, ![]() , and
, and ![]() . Notice that the variables eps and tscale are internally set to their default values. For more information about the NLPDD subroutine
, see the section NLPDD Call. For details about the opt, tc, and par arguments in the NLPDD call
, see the section Options Vector, the section Termination Criteria, and the section Control Parameters Vector, respectively.
. Notice that the variables eps and tscale are internally set to their default values. For more information about the NLPDD subroutine
, see the section NLPDD Call. For details about the opt, tc, and par arguments in the NLPDD call
, see the section Options Vector, the section Termination Criteria, and the section Control Parameters Vector, respectively.
You can replicate other values in Table 2 of Wang and Tsiatis (1987) by changing the values of the variables NL and PLEVEL. You can obtain values from Table 3 by changing the value of the variable LEVEL to 0.99 and specifying NL and PLEVEL accordingly.
This example illustrates how to find the boundaries that minimize ASN given the required significance level and the required power. It replicates some of the results published in Table 3 of Pocock (1982). The program computes the domain that
-
minimizes the ASN
-
yields a given significance level of 0.05
-
yields a given power
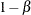 under the alternative hypothesis
under the alternative hypothesis
The last two nonlinear conditions on the optimization process can be incorporated as a penalty applied on the error in these nonlinear conditions. The following program does the computations for a power of 0.9.
%let nl=5;
proc iml;
start func(m) global(level,plevel,sigma,epss,
geometry,stgeom,gscale,mean,alpha,beta,tn,asn);
m = abs(m);
mm = ( -m // m)*sigma;
/* meet the significance level */
call seqscale(prob,gscale,mm,level) iguess=gscale eps=epss;
stgeom = gscale*m;
geometry= mm*gscale;
alpha = (prob[2,]-prob[1,])[&nl];
/* meet the power condition */
call seqshift(prob,mean,geometry,plevel) iguess=mean eps=epss;
beta = (prob[2,]-prob[1,])[&nl];
p = prob[3,] - prob[2,]+prob[1,];
/* compute the average sample number */
tn = 4*mean##2; /* number per group */
asn = tn *( &nl - p *((&nl-1):0)`);
return(asn);
finish;
/* set up the global variables needed by func */
epss = 1.e-8;
epso = 1.e-5;
level = 9.50000E-01;
plevel = 0.05;
sigma = diag(sqrt(1:5));
/* set up options used to control the optimization routine */
opt = {0 2 0 1 6};
tc = repeat(.,1,12);
tc[1] = 100;
tc[7] = 1.e-4;
par = { 1.e-13 . 1.e-10 . . .} || . || epso;
/* provide the constraint matrix to ensure monotonically
increasing significance levels */
con = { . . . . . . . ,
. . . . . . . ,
1 -1 . . . 1 0 ,
. 1 -1 . . 1 0 ,
. . 1 -1 . 1 0 ,
. . . 1 -1 1 0 };
/* provide the initial guess and call nlpdd */
m = { 1 1 1 1 1 };
call nlpdd(rc,rx,"func",m) opt=opt blc = con tc=tc par=par;
print stgeom;
Although eps has been set to eps=![]() , tscale has been internally set to its default value. You can choose to run the program with and without the specification of the
keyword IGUESS to see the effect on the execution time.
, tscale has been internally set to its default value. You can choose to run the program with and without the specification of the
keyword IGUESS to see the effect on the execution time.
Notice the following about the optimization process:
-
Different levels of precision are imposed on different modules. In this example, epss, which is used as the precision for the sequential tests, is 1E
 8. The absolute and relative function criteria for the objective function are set to par[7]=1E
8. The absolute and relative function criteria for the objective function are set to par[7]=1E 5 and tc[7]=1E
5 and tc[7]=1E 4, respectively. Since finite differences are used to compute the first and second derivatives, the sequential test should
be more precise than the optimization routine. Otherwise, the finite difference estimation is worthless. Optimally, if the
precision of the function evaluation is
4, respectively. Since finite differences are used to compute the first and second derivatives, the sequential test should
be more precise than the optimization routine. Otherwise, the finite difference estimation is worthless. Optimally, if the
precision of the function evaluation is 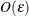 , the first- and second-order derivatives should be estimated with perturbations
, the first- and second-order derivatives should be estimated with perturbations 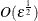 and
and 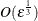 , respectively. For example, if all three precision levels are set to 1E
, respectively. For example, if all three precision levels are set to 1E 5, the optimization process does not work properly.
5, the optimization process does not work properly.
-
Line search techniques that do not depend on the computation of the derivative are preferable.
-
The amount of printed information from the optimization routines is controlled by opt[2] and can be set to any value between 0 and 3. Larger numbers produce more output.