Language Reference

QUAD Call

Subsections:

A Simple Example
Using the PEAK= Option
Using the SCALE= Option
Two-Dimensional Integration

CALL QUAD (r, "fun", points <*>, eps <*>, peak <*>, scale <*>, msg <*>, cycles );

The QUAD subroutine performs numerical integration of scalar functions in one dimension over infinite, connected semi-infinite, and connected finite intervals.

The QUAD subroutine returns the following value:

r: is a numeric vector that contains the results of the integration. The size of r is equal to the number of subintervals defined by the argument points. If the numerical integration fails on a particular subinterval, the corresponding element of r is set to missing.

The input arguments to the QUAD subroutine are as follows:

"fun": specifies the name of a module used to evaluate the integrand.
points: specifies a sorted vector that provides the limits of integration over connected subintervals. The simplest form of the vector provides the limits of the integration on one interval. The first element of points should contain the left limit. The second element should be the right limit. A missing value of .M in the left limit is interpreted as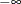 $-\infty$ , and a missing value of .P is interpreted as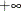 $+\infty$ . For more advanced usage of the QUAD call, points can contain more than two elements. The elements of the vector must be sorted in an ascending order. Each two consecutive elements in points defines a subinterval, and the subroutine reports the integration over each specified subinterval. The use of subintervals is important because the presence of internal points of discontinuity in the integrand hinders the algorithm.
eps: is an optional scalar that specifies the desired relative accuracy. It has a default value of 1E $-$ 7. You can specify eps by using the EPS= keyword.
peak: is an optional scalar that is the approximate location of a maximum of the integrand. By default, it has a location of 0 for infinite intervals, a location that is one unit away from the finite boundary for semi-infinite intervals, and a centered location for bounded intervals. You can specify peak by using the PEAK= keyword.
scale: is an optional scalar that is the approximate estimate of any scale in the integrand along the independent variable (see the examples). It has a default value of 1. You can specify scale by using the SCALE= keyword.
msg: is an optional character scalar that restricts the number of messages produced by the QUAD subroutine. If msg = "NO" then it does not produce any warning messages. You can specify msg by using the MSG= keyword.
cycles: is an optional integer that indicates the maximum number of refinements the QUAD subroutine can make in order to achieve the required accuracy. It has a default value of 8. You can specify cycles by using the CYCLES= keyword.

If the dimensions of any optional argument are $0 \times 0$ , the QUAD subroutine uses its default value.

The QUAD subroutine is a numerical integrator based on adaptive Romberg-type integration techniques. See Rice (1973), Sikorsky (1982), Sikorsky and Stenger (1984), Stenger (1973a), Stenger (1973b), and Stenger (1978). Many adaptive numerical integration methods (Ralston and Rabinowitz, 1978) start at one end of the interval and proceed towards the other end, working on subintervals while locally maintaining a certain prescribed precision. This is not the case with the QUAD call. The QUAD subroutine is an adaptive global-type integrator that produces a quick, rough estimate of the integration result and then refines the estimate until it achieves the prescribed accuracy. This gives the subroutine an advantage over Gauss-Hermite and Gauss-Laguerre quadratures (Ralston and Rabinowitz, 1978; Squire, 1987), particularly for infinite and semi-infinite intervals, because those methods perform only a single evaluation.

A Simple Example

Consider the integral

$\int _0^{\infty } e^{-t} ~ dt$

The following statements evaluate this integral:

/* Define the integrand */
start fun(t);
   v = exp(-t);
   return(v);
finish;

a = {0  .P};
call quad(z, "fun", a);
print z[format=E21.14];

Figure 24.287: Result of Numerical Integration on a Semi-Infinite Domain

z
9.99999999595190E-01

The integration is carried out over the interval $(0,\infty )$ , as specified by the a variable. The missing value in the second element of a is interpreted as $\infty$ . The values of EPS=1E $-$ 7, PEAK=1, SCALE=1, and CYCLES=8 are used by default.

The following statements integrate the same exponential function over two subintervals:

a   = {0  3 .P };
call quad(z2, "fun", a);
print z2[format=E21.14];

Figure 24.288: Result of Numerical Integration on Two Intervals

z2
9.50212930994570E-01
4.97870683477090E-02

Notice that the elements of a are in ascending order. The integration is carried out over $(0,3)$ and $(3,\infty )$ , and the corresponding results are shown in the output. The values of EPS=1E $-$ 7, PEAK=1, SCALE=1, and CYCLES=8 are used by default. To obtain the results of integration over $(0,\infty )$ , use the SUM function on the elements of the z2 vector, as follows:

 b = sum(z2);
 print b[format=E21.14];

Figure 24.289: Result of Numerical Integration on Two Intervals

b
9.99999999342280E-01

Using the PEAK= Option

The peak and scale options enable you to avoid analytically changing the variable of the integration in order to produce a well-conditioned integrand that permits the numerical evaluation of the integration.

Consider the integration

$\int _0^{\infty } e^{-10000t} ~ dt$

The following statements evaluate this integral:

start fun2(t);
   v = exp(-10000*t);
   return(v);
finish;

a = {0  .P};
/* Either syntax can be used                    */
/*   call quad(z, "fun2", a, 1E-10, 0.0001); or */
call quad(z3, "fun2", a) eps=1E-10 peak=0.0001;
print z3[format=E21.14];

Figure 24.290: Result of Specifying PEAK= Option

z3
9.99999999998990E-05

The integration is performed over the semi-infinite interval $(0,\infty )$ . The default values of SCALE=1 and CYCLES=8 are used. However, the default value of peak is 1 for this semi-infinite interval, which is not a good estimate of the location of the function’s maximum. If you do not specify a peak value, the integration cannot be evaluated to the desired accuracy, a message is printed to the LOG, and a missing value is returned. Note that peak can still be set to 1E $-$ 7 and the integration will be successful.

The evaluation of the integrand at peak must be nonzero for the computation to continue. You should adjust the value of peak to get a nonzero evaluation at peak before trying to adjust scale. Reducing scale decreases the initial step size and can lead to an increase in the number of function evaluations per step at a linear rate.

Using the SCALE= Option

Consider the integration

$\int _{-\infty }^{\infty } e^{-100000(t-3)^2} ~ dt$

The integrand is essentially zero except on a small interval close to $t=3$ . The following statements evaluate this integral:

/* Define the integrand */
start fun3(t);
   v = exp(-100000*(t-3)*(t-3));
   return(v);
finish;

a = { .M  .P };
call quad(z4, "fun3", a) eps=1E-10 peak=3 scale=0.001;
print z4[format=E21.14];

Figure 24.291: Result of Specifying the SCALE= Option

z4
5.60499121639830E-03

The integration is carried out over the infinite interval $(-\infty ,\infty )$ . The default value of CYCLES=8 has been used. The integrand has its maximum value at $t=3$ , so the PEAK=3 option is specified.

If you use the default value of scale, the integral cannot be evaluated to the desired accuracy, and a missing value is returned. The variables scale and cycles can be used to increase the number of possible function evaluations; the number of possible function evaluations increases linearly with the reciprocal of scale, but it potentially increases in an exponential manner when cycles is increased. Increasing the number of function evaluations increases execution time.

Two-Dimensional Integration

When you perform double integration, you must separate the variables between the iterated integrals. There should be a clear distinction between the variable of the one-dimensional integration and the parameters that are passed to the integrand. Another important consideration is specifying the correct limits of integration.

For example, suppose you want to compute probabilities for the standard bivariate normal distribution with correlation $\rho$ . In particular, if an observation $(x,y)$ is drawn from the distribution, what is probability that $x\leq a$ and $y\leq b$ for given values of a and b?

The bivariate normal probability is given by the following double integral:

$\mbox{probbnrm}(a,b,\rho ) = \frac{1}{2\pi \sqrt {1-\rho ^2}} \int _{-\infty }^ a \int _{-\infty }^ b \exp \left( -\frac{x^2 - 2 \rho xy + y^2}{2(1 - \rho ^2)} \right) ~ dy ~ dx$

The inner integral is

$g(x,b,\rho ) = \frac{1}{2 \pi \sqrt {1 - \rho ^2}} \int _{-\infty }^ b \exp \left( -\frac{x^2 - 2 \rho xy+y^2}{2(1-\rho ^2)} \right) ~ dy$

with parameters x and $\rho$ , and the limits of integration are from $-\infty$ to b. The outer integral is then

$\mbox{probbnrm}(a,b,\rho ) = \int _{-\infty }^ a g(x,b,\rho ) ~ dx$

with the limits from $-\infty$ to a.

You can write a function module with parameters $a, b, \rho$ that computes the bivariate normal probability. In the following statements, the function module is called NORCDF2 because it compute the CDF of the bivariate normal distribution. The NORCDF2 module calls the QUAD subroutine on the MARGINAL module, which computes the outer integral. The MARGINAL module, in turn, uses the QUAD function to evaluate inner integral. The integrand of the inner integral is defined in the NORPDF2 module.

/*-----------------------------------------------------*/
/* This function is the density function and requires  */
/* the variable T (passed in the argument)             */
/* and a list of global parameters, YV, RHO, COUNT     */
/*-----------------------------------------------------*/
start norpdf2(t) global(yv,rho,count);
   count = count+1;
   q=(t#t-2#rho#t#yv+yv#yv)/(1-rho#rho);
   p=exp(-q/2);
   return(p);
finish;

/*--------------------------------------------------*/
/* The outer integral                               */
/* The limits of integration are .M to YY           */
/* YV is passed as a parameter to the inner integral*/
/*--------------------------------------------------*/
start marginal(v) global(yy,yv,eps);
   interval = .M || yy;
   if ( v < -12 ) then return(0);
   yv = v;
   call quad(pm, "NORPDF2", interval) eps=eps;
   return(pm);
finish;

/*------------------------------------------------*/
/* Global parameters: YY, RHO, EPS                */
/* EPS is set from IML                            */
/*------------------------------------------------*/
start norcdf2(a, b, rrho) global(yy,rho,eps);
   rho = rrho; /* copy arguments (local variables) to global list */
   yy = b;

   interval= .M || a; /* upper/lower limits for outer integral */
   call quad(p,"MARGINAL",interval) eps=eps;

   pi = constant("Pi");
   per = p /(2#pi#sqrt(1-rho#rho)); /* scale the value from QUAD */
   return(per);
finish;

/*-----------------------------------------------------*/
/* Main Program: set up global constants and call QUAD */
/*-----------------------------------------------------*/
count = 0;
eps = 1E-11;

p =  norcdf2(2, 1, 0.1);
print p[format=E21.14], count;

Figure 24.292: Result of Numerical Integration of a Double Iterated Integral

p
8.23640898880300E-01

count
250453

The variable COUNT contains the number of times the NORPDF2 module is called. Note that the value computed by the NORCDF2 module is very close to that returned by the PROBBNRM function, which computes probabilites for the bivariate normal model, as shown by the following statements:

/* Compute the value with the PROBBNRM function */
pp = probbnrm(2,1,0.1);
print pp[format=E21.14];

Figure 24.293: Result of Numerical Integration of a Double Iterated Integral

pp
8.23640898880500E-01

Note the following:

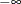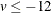The iterated inner integral cannot have a left endpoint of $-\infty$ . For large values of v, the inner integral does not contribute to the answer but still needs to be computed to the required relative accuracy. Therefore, either cut off the function (when $v \leq -12$ ), as in the MARGINAL module in the preceding example, or have the intervals start from a reasonable cutoff value. In addition, the QUAD subroutine stops if the integrands appear to be identically 0 (probably caused by underflow) over the interval of integration.
This method of integration (iterated, one-dimensional integrals) is extremely conservative and requires unnecessary function evaluations. In this example, the QUAD subroutine for the inner integration lacks information about the final value that the QUAD subroutine for the outer integration is trying to refine. The lack of communication between the two QUAD routines can cause useless computations to be performed in the inner integration.

To illustrate this idea, let the relative error be 1E $-$ 11 and let the answer delivered by the outer integral be close to 0.8, as in this example. Any computation of the inner execution of the QUAD call that yields 0.8E $-$ 11 or less does not contribute to the final answer of the QUAD subroutine for the outer integral. 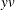However, the inner integral lacks this information, and for a given value of the parameter $yv$ , it attempts to compute an answer with much more precision than is necessary. The lack of communication between the two QUAD subroutines prevents the introduction of better cutoffs. Although this method can be inefficient, the final calculations are accurate.