Orthogonal Regression :: SAS/IML(R) 13.1 User's Guide

Orthogonal Regression

In the previous section, you ran a module that computes parameter estimates and statistics for a linear regression model. All of the matrices used in the Regress module are global variables because the Regress module does not have any arguments. Consequently, you can use those matrices in additional calculations.

Suppose you want to correlate the parameter estimates. To do this, you can calculate the covariance of the estimates, then scale the covariance into a correlation matrix with values of 1 on the diagonal. The following statements perform these operations:

covb = xpxi*mse;              /* covariance of estimates */
s = 1/sqrt(vecdiag(covb));    /* standard errors */
corrb = diag(s)*covb*diag(s); /* correlation of estimates */
print covb, s, corrb;

The results are shown in Figure 4.6. The covariance matrix of the estimates is contained in the covb matrix. The vector s contains the standard errors of the parameter estimates and is used to compute the correlation matrix of the estimates (corrb).

Equivalently, you can form the covb matrix and then call the COV2CORR function in order to generate the corrb matrix: corrb = cov2corr(covb).

Figure 4.6: Covariance and Correlation Matrices for Estimates

Regression Results
SSE	DFE	MSE	RSquare
6.4	2	3.2	0.9923518

Parameter Estimates
Estimate	StdErr	t	Pr>\|t\|
2.4	3.8367	0.6255	0.5955
-3.2	2.9238	-1.094	0.388
2	0.4781	4.1833	0.0527

y	yhat	resid
1	1.2	-0.2
5	4	1
9	10.8	-1.8
23	21.6	1.4
36	36.4	-0.4

covb
14.72	-10.56	1.6
-10.56	8.5485714	-1.371429
1.6	-1.371429	0.2285714

s
0.260643
0.3420214
2.0916501

corrb
1	-0.941376	0.8722784
-0.941376	1	-0.981105
0.8722784	-0.981105	1

You can also use the Regress module to carry out an orthogonalized regression version of the previous polynomial regression. In general, the columns of 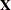$\mb {X}$ are not orthogonal. You can use the ORPOL function to generate orthogonal polynomials for the regression. Using them provides greater computing accuracy and reduced computing times. When you use orthogonal polynomial regression, you can expect the statistics of fit to be the same and expect the estimates to be more stable and uncorrelated.

To perform an orthogonal regression on the data, you must first create a vector that contains the values of the independent variable $x$ , which is the second column of the design matrix 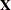$\mb {X}$ . Then, use the ORPOL function to generate orthogonal second degree polynomials. The following statements perform these operations:

x1 = x[,2];                   /* data = second column of X */
x = orpol(x1, 2);             /* generate orthogonal polynomials */
run Regress;                  /* run Regress module */

covb = xpxi*mse;              /* covariance of estimates */
s = 1 / sqrt(vecdiag(covb));
corrb = diag(s)*covb*diag(s);
print covb, s, corrb;

Figure 4.7: Covariance and Correlation Matrices for Estimates

Regression Results
SSE	DFE	MSE	RSquare
6.4	2	3.2	0.9923518

Parameter Estimates
Estimate	StdErr	t	Pr>\|t\|
33.094	1.7889	18.5	0.0029
27.828	1.7889	15.556	0.0041
7.4833	1.7889	4.1833	0.0527

y	yhat	resid
1	1.2	-0.2
5	4	1
9	10.8	-1.8
23	21.6	1.4
36	36.4	-0.4

covb
3.2	0	0
0	3.2	0
0	0	3.2

s
0.559017
0.559017
0.559017

corrb
1	0	0
0	1	0
0	0	1

For these data, the off-diagonal values of the corrb matrix are displayed as zeros. For some analyses you might find that certain matrix elements are very close to zero but not exactly zero because of the computations of floating-point arithmetic. You can use the RESET FUZZ option to control whether small values are printed as zeros.