Example 14.2 Network Flow and Delay :: SAS/IML(R) 13.1 User's Guide

Example 14.2 Network Flow and Delay

The following example is taken from the user’s guide of the GINO program (Liebman et al., 1986). A simple network of five roads (arcs) can be illustrated by a path diagram.

The five roads connect four intersections illustrated by numbered nodes. Each minute, $F$ vehicles enter and leave the network. The parameter $x_{ij}$ refers to the flow from node $i$ to node $j$ . The requirement that traffic that flows into each intersection $j$ must also flow out is described by the linear equality constraint

$\sum _ i x_{ij} = \sum _ i x_{ji} \quad , \quad j=1,\ldots ,n$

In general, roads also have an upper limit on the number of vehicles that can be handled per minute. These limits, denoted $c_{ij}$ , can be enforced by boundary constraints:

$0 \le x_{ij} \le c_{ij}$

The goal in this problem is to maximize the flow, which is equivalent to maximizing the objective function $f(x)$ , where $f(x)$ is

$f(x) = x_{24} + x_{34}$

The boundary constraints are

$\begin{eqnarray*} 0 \le & x_{12}, x_{32}, x_{34} & \le 10 \\ 0 \le & x_{13}, x_{24} & \le 30 \\ \end{eqnarray*}$

and the flow constraints are

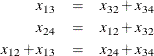
$\begin{eqnarray*} x_{13} & = & x_{32} + x_{34} \\ x_{24} & = & x_{12} + x_{32} \\ x_{12} + x_{13} & = & x_{24} + x_{34} \end{eqnarray*}$

The three linear equality constraints are linearly dependent. One of them is deleted automatically by the optimization subroutine. The following notation is used in this example:

$X1=x_{12},~ ~ X2=x_{13},~ ~ X3=x_{32},~ ~ X4=x_{24},~ ~ X5=x_{34}$

Even though the NLPCG subroutine is used, any other optimization subroutine would also solve this small problem. The following code finds the maximum flow:

   proc iml;
      title 'Maximum Flow Through a Network';
      start MAXFLOW(x);
         f = x[4] + x[5];
         return(f);
      finish MAXFLOW;

      con = {  0.  0.  0.  0.  0.   .   . ,
              10. 30. 10. 30. 10.   .   . ,
               0.  1. -1.  0. -1.  0.  0. ,
               1.  0.  1. -1.  0.  0.  0. ,
               1.  1.  0. -1. -1.  0.  0. };
      x = j(1,5, 1.);
      optn = {1 3};
      call nlpcg(xres,rc,"MAXFLOW",x,optn,con);

The optimal solution is shown in the following output.

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Active Bound Constraint
1	X1	10.000000	0	Upper BC
2	X2	10.000000	0
3	X3	10.000000	1.000000	Upper BC
4	X4	20.000000	1.000000
5	X5	-1.11022E-16	0	Lower BC

Finding the maximum flow through a network is equivalent to solving a simple linear optimization problem, and for large problems, the LP procedure or the NETFLOW procedure of the SAS/OR product can be used. On the other hand, finding a traffic pattern that minimizes the total delay to move $F$ vehicles per minute from node 1 to node 4 includes nonlinearities that need nonlinear optimization techniques. As traffic volume increases, speed decreases. Let $t_{ij}$ be the travel time on arc $(i,j)$ and assume that the following formulas describe the travel time as decreasing functions of the amount of traffic:

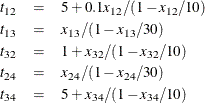
$\begin{eqnarray*} t_{12} & = & 5 + 0.1 x_{12} / (1 - x_{12}/10) \\ t_{13} & = & x_{13} / (1 - x_{13}/30) \\ t_{32} & = & 1 + x_{32} / (1 - x_{32}/10) \\ t_{24} & = & x_{24} / (1 - x_{24}/30) \\ t_{34} & = & 5 + x_{34} / (1 - x_{34}/10) \end{eqnarray*}$

These formulas use the road capacities (upper bounds), and you can assume that $F=5$ vehicles per minute have to be moved through the network. The objective is now to minimize

$f =f(x)= t_{12} x_{12} + t_{13} x_{13} + t_{32} x_{32} + t_{24} x_{24} + t_{34} x_{34}$

The constraints are

$\begin{eqnarray*} 0 \le & x_{12}, x_{32}, x_{34} & \le 10 \\ 0 \le & x_{13}, x_{24} & \le 30 \\ \end{eqnarray*}$

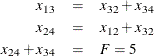
$\begin{eqnarray*} x_{13} & = & x_{32} + x_{34} \\ x_{24} & = & x_{12} + x_{32} \\ x_{24} + x_{34} & = & F = 5 \end{eqnarray*}$

In the following code, the NLPNRR subroutine is used to solve the minimization problem:

   proc iml;
      title 'Minimize Total Delay in Network';
      start MINDEL(x);
         t12 = 5. + .1 * x[1] / (1. - x[1] / 10.);
         t13 = x[2] / (1. - x[2] / 30.);
         t32 = 1. + x[3] / (1. - x[3] / 10.);
         t24 = x[4] / (1. - x[4] / 30.);
         t34 = 5. + .1 * x[5] / (1. - x[5] / 10.);
         f = t12*x[1] + t13*x[2] + t32*x[3] + t24*x[4] + t34*x[5];
         return(f);
      finish MINDEL;

      con = {  0.  0.  0.  0.  0.   .   . ,
              10. 30. 10. 30. 10.   .   . ,
               0.  1. -1.  0. -1.  0.  0. ,
               1.  0.  1. -1.  0.  0.  0. ,
               0.  0.  0.  1.  1.  0.  5. };

      x = j(1,5, 1.);
      optn = {0 3};
      call nlpnrr(xres,rc,"MINDEL",x,optn,con);

The optimal solution is shown in the following output.

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Active Bound Constraint
1	X1	2.500001	5.777778
2	X2	2.499999	5.702478
3	X3	-5.55112E-17	1.000000	Lower BC
4	X4	2.500001	5.702481
5	X5	2.499999	5.777778

The active constraints and corresponding Lagrange multiplier estimates (costs) are shown in the following output.

Linear Constraints Evaluated at Solution
1	ACT	-4.441E-16	=	0	+	1.0000	*	X2	-	1.0000	*	X3	-	1.0000	*	X5
2	ACT	4.4409E-16	=	0	+	1.0000	*	X1	+	1.0000	*	X3	-	1.0000	*	X4
3	ACT	4.4409E-16	=	-5.0000	+	1.0000	*	X4	+	1.0000	*	X5

First Order Lagrange Multipliers
Active Constraint		Lagrange Multiplier
Lower BC	X3	0.924702
Linear EC	[1]	5.702479
Linear EC	[2]	5.777777
Linear EC	[3]	11.480257