If the optimization technique needs first- or second-order derivatives and you do not specify the corresponding IML module
“grd,” “hes,” “jac,” or “jacnlc,” the derivatives are approximated by finite-difference formulas using only calls of the module “fun.” If the optimization technique needs second-order derivatives and you specify the “grd” module but not the “hes” module, the subroutine approximates the second-order derivatives by finite differences using ![]() or
or ![]() calls of the “grd” module.
calls of the “grd” module.
The eighth element of the opt argument specifies the type of finite-difference approximation used to compute first- or second-order derivatives and whether
the finite-difference intervals, ![]() , should be computed by an algorithm of Gill et al. (1983). The value of opt[8] is a two-digit integer,
, should be computed by an algorithm of Gill et al. (1983). The value of opt[8] is a two-digit integer, ![]() .
.
-
If opt[8] is missing or
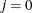 , the fast but not very precise forward-difference formulas are used; if
, the fast but not very precise forward-difference formulas are used; if 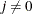 , the numerically more expensive central-difference formulas are used.
, the numerically more expensive central-difference formulas are used.
-
If opt[8] is missing or
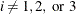 , the finite-difference intervals
, the finite-difference intervals 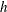 are based only on the information of par[8] or par[9], which specifies the number of accurate digits to use in evaluating the objective function and nonlinear constraints,
respectively. If
are based only on the information of par[8] or par[9], which specifies the number of accurate digits to use in evaluating the objective function and nonlinear constraints,
respectively. If 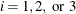 , the intervals are computed with an algorithm by Gill et al. (1983). For
, the intervals are computed with an algorithm by Gill et al. (1983). For 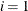 , the interval is based on the behavior of the objective function; for
, the interval is based on the behavior of the objective function; for 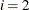 , the interval is based on the behavior of the nonlinear constraint functions; and for
, the interval is based on the behavior of the nonlinear constraint functions; and for 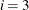 , the interval is based on the behavior of both the objective function and the nonlinear constraint functions.
, the interval is based on the behavior of both the objective function and the nonlinear constraint functions.
-
First-order derivatives:
 additional function calls are needed.
additional function calls are needed.
![\[ g_ i = {\partial f \over \partial x_ i} = {f(x + h_ ie_ i) - f(x) \over h_ i} \]](images/imlug_nonlinearoptexpls0088.png)
-
Second-order derivatives based on function calls only, when the “grd” module is not specified (Dennis and Schnabel, 1983): for a dense Hessian matrix,
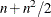 additional function calls are needed.
additional function calls are needed.
![\[ {\partial ^2 f \over \partial x_ i \partial x_ j} = {f(x+h_ ie_ i+h_ je_ j) - f(x+h_ ie_ i) - f(x+h_ je_ j) + f(x) \over h_ i h_ j} \]](images/imlug_nonlinearoptexpls0090.png)
-
Second-order derivatives based on gradient calls, when the “grd” module is specified (Dennis and Schnabel, 1983):
 additional gradient calls are needed.
additional gradient calls are needed.
![\[ {\partial ^2 f \over \partial x_ i \partial x_ j} = {g_ i(x + h_ je_ j) - g_ i(x) \over 2h_ j} + {g_ j(x + h_ ie_ i) - g_ j(x) \over 2h_ i} \]](images/imlug_nonlinearoptexpls0091.png)
-
First-order derivatives:
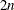 additional function calls are needed.
additional function calls are needed.
![\[ g_ i = {\partial f \over \partial x_ i} = {f(x + h_ ie_ i) - f(x - h_ ie_ i) \over 2h_ i} \]](images/imlug_nonlinearoptexpls0092.png)
-
Second-order derivatives based on function calls only, when the “grd” module is not specified (Abramowitz and Stegun, 1972): for a dense Hessian matrix,
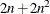 additional function calls are needed.
additional function calls are needed.
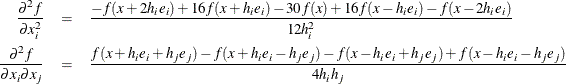
-
Second-order derivatives based on gradient calls, when the “grd” module is specified:
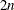 additional gradient calls are needed.
additional gradient calls are needed.
![\[ {\partial ^2 f \over \partial x_ i \partial x_ j} = {g_ i(x + h_ je_ j) - g_ i(x - h_ je_ j) \over 4h_ j} + {g_ j(x + h_ ie_ i) - g_ j(x - h_ ie_ i) \over 4h_ i} \]](images/imlug_nonlinearoptexpls0095.png)
The step sizes ![]() ,
, ![]() , are defined as follows:
, are defined as follows:
-
For the forward-difference approximation of first-order derivatives using only function calls and for second-order derivatives using only gradient calls,
![$h_ j = \sqrt [2]{\eta _ j} (1 + |x_ j|)$](images/imlug_nonlinearoptexpls0098.png) .
.
-
For the forward-difference approximation of second-order derivatives using only function calls and for central-difference formulas,
![$h_ j = \sqrt [3]{\eta _ j} (1 + |x_ j|)$](images/imlug_nonlinearoptexpls0099.png) .
.
If the algorithm of Gill et al. (1983) is not used to compute ![]() , a constant value
, a constant value ![]() is used depending on the value of par[8].
is used depending on the value of par[8].
-
If the number of accurate digits is specified by par
![$[8]=k_1$](images/imlug_nonlinearoptexpls0102.png) , then
, then 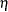 is set to
is set to 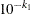 .
.
-
If par[8] is not specified,
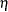 is set to the machine precision,
is set to the machine precision,  .
.
If central-difference formulas are not specified, the optimization algorithm switches automatically from the forward-difference formula to a corresponding central-difference formula during the iteration process if one of the following two criteria is satisfied:
-
The absolute maximum gradient element is less than or equal to 100 times the ABSGTOL threshold.
-
The term on the left of the GTOL criterion is less than or equal to
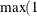 E
E 6,
6, 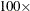 GTOL threshold
GTOL threshold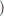 . The 1E
. The 1E 6 ensures that the switch is performed even if you set the GTOL threshold to zero.
6 ensures that the switch is performed even if you set the GTOL threshold to zero.
The algorithm of Gill et al. (1983) that computes the finite-difference intervals ![]() can be very expensive in the number of function calls it uses. If this algorithm is required, it is performed twice, once
before the optimization process starts and once after the optimization terminates.
can be very expensive in the number of function calls it uses. If this algorithm is required, it is performed twice, once
before the optimization process starts and once after the optimization terminates.
Many applications need considerably more time for computing second-order derivatives than for computing first-order derivatives. In such cases, you should use a quasi-Newton or conjugate gradient technique.
If you specify a vector, ![]() , of
, of ![]() nonlinear constraints with the “nlc” module but you do not specify the “jacnlc” module, the first-order formulas can be used to compute finite-difference approximations of the
nonlinear constraints with the “nlc” module but you do not specify the “jacnlc” module, the first-order formulas can be used to compute finite-difference approximations of the ![]() Jacobian matrix of the nonlinear constraints.
Jacobian matrix of the nonlinear constraints.
You can specify the number of accurate digits in the constraint evaluations with par[9]. This specification also defines the step sizes ![]() ,
, ![]() .
.
Note: If you are not able to specify analytic derivatives and if the finite-difference approximations provided by the subroutines are not good enough to solve your optimization problem, you might be able to implement better finite-difference approximations with the “grd,” “hes,” “jac,” and “jacnlc” module arguments.