Kuhn-Tucker Conditions :: SAS/IML(R) 13.1 User's Guide

Kuhn-Tucker Conditions

The nonlinear programming (NLP) problem with one objective function $f$ and $m$ constraint functions $c_ i$ , which are continuously differentiable, is defined as follows:

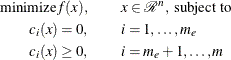
$\begin{eqnarray*} \mbox{minimize} f(x), & & x \in \mathcal{R}^ n, \; \mbox{subject to} \\ c_ i(x) = 0 , & & i = 1,\ldots ,m_ e \\ c_ i(x) \ge 0 , & & i = m_ e+1,\ldots ,m \end{eqnarray*}$

In the preceding notation, $n$ is the dimension of the function $f(x)$ , and $m_ e$ is the number of equality constraints. The linear combination of objective and constraint functions

$L(x,\lambda ) = f(x) - \sum _{i=1}^ m \lambda _ i c_ i(x)$

is the Lagrange function, and the coefficients $\lambda _ i$ are the Lagrange multipliers.

If the functions $f$ and $c_ i$ are twice differentiable, the point $x^*$ is an isolated local minimizer of the NLP problem, if there exists a vector $\lambda ^*=(\lambda _1^*, \ldots ,\lambda _ m^*)$ that meets the following conditions:

Kuhn-Tucker conditions

$\begin{array}{ll} c_ i(x^*) = 0 , & i = 1, \ldots ,m_ e \\ c_ i(x^*) \ge 0 , ~ ~ \lambda _ i^* \ge 0, ~ ~ \lambda _ i^* c_ i(x^*) = 0 , & i = m_ e+1, \ldots ,m \\ \nabla _ x L(x^*,\lambda ^*) = 0 \end{array}$
second-order condition

Each nonzero vector 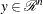$y \in \mathcal{R}^ n$ with

$y^ T \nabla _ x c_ i(x^*) = 0 i = 1,\ldots ,m_ e ,\; \mbox{ and } \forall i\in {m_ e+1,\ldots ,m}; \lambda _ i^* > 0$

satisfies

$y^ T \nabla _ x^2 L(x^*,\lambda ^*) y > 0$

In practice, you cannot expect the constraint functions $c_ i(x^*)$ to vanish within machine precision, and determining the set of active constraints at the solution $x^*$ might not be simple.