VARMACOV Call :: SAS/IML(R) 13.1 User's Guide

VARMACOV Call

CALL VARMACOV (cov, phi, theta, sigma <*>, p <*>, q <*>, lag ) ;

The VARMACOV subroutine computes the theoretical cross-covariance matrices for a stationary VARMA( $p,q$ ) model.

The input arguments to the VARMACOV subroutine are as follows:

phi

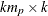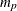specifies a $km_ p \times k$ matrix, $\Phi$ , that contains the autoregressive coefficient matrices, where $m_ p$ is the number of elements in the subset of the AR order and 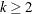$k\geq 2$ is the number of variables. All the roots of 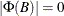$|\Phi (B)|=0$ should be greater than one in absolute value, where 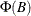$\Phi (B)$ is the finite order matrix polynomial in the backshift operator 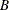$B$ , such that 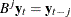$B^ j\mb {y}_{t}=\mb {y}_{t-j}$ . You must specify either phi or theta.

theta

specifies a 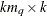$km_ q \times k$ matrix that contains the moving average coefficient matrices, where 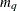$m_ q$ is the number of the elements in the subset of the MA order. You must specify either phi or theta.

sigma

specifies a 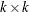$k \times k$ symmetric positive-definite covariance matrix of the innovation series. If sigma is not specified, then an identity matrix is used.

p

specifies the subset of the AR order. The quantity 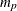$m_ p$ is defined as

$m_ p={ nrow(phi)/ncol(phi) }$

where nrow(phi) is the number of rows of the matrix phi and ncol(phi) is the number of columns of the matrix phi.

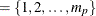If you do not specify p, the default subset is p $=\{ 1,2,\ldots ,m_ p\}$ .

For example, consider a 4-dimensional vector time series, and phi is a 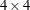$4 \times 4$ matrix. If you specify p=1 (the default, since 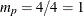$m_ p=4/4=1$ ), the VARMACOV subroutine computes the theoretical cross-covariance matrices of VAR(1) as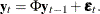 $\mb {y}_ t = \Phi \mb {y}_{t-1} + \bm {\epsilon }_ t.$

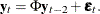
If you specify p=2, the VARMACOV subroutine computes the cross-covariance matrices of VAR(2) as $\mb {y}_ t = \Phi \mb {y}_{t-2} + \bm {\epsilon }_ t.$

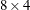Let phi $= [ \Phi _1’, ~ \Phi _2’ ]’$ be an $8\times 4$ matrix. If you specify p 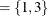$=\{ 1,3\}$ , the VARMACOV subroutine computes the cross-covariance matrices of VAR(3) as 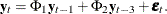$\mb {y}_ t=\Phi _1\mb {y}_{t-1}+\Phi _2\mb {y}_{t-3}+\bm {\epsilon }_ t.$ If you do not specify p, the VARMACOV subroutine computes the cross-covariance matrices of VAR(2) as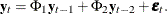 $\mb {y}_ t=\Phi _1\mb {y}_{t-1}+\Phi _2 \mb {y}_{t-2}+\bm {\epsilon }_ t.$

q

specifies the subset of the MA order. The quantity 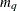$m_ q$ is defined as

$m_ q={ nrow(theta)/ncol(theta) }$

where nrow(theta) is the number of rows of matrix theta and ncol(theta) is the number of columns of matrix theta.

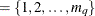If you do not specify q, the default subset is q $=\{ 1,2,\ldots ,m_ q\}$ .

The usage of q is the same as that of p.

lag

specifies the length of lags, which must be a positive number. If 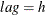$lag = h$ , the VARMACOV computes the cross-covariance matrices from lag zero to lag 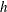$h$ . By default, lag = 12.

The VARMACOV subroutine returns the following value:

cov: is a 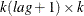$k(lag+1)\times k$ matrix that contains the theoretical cross-covariance matrices of the VARMA( 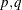$p,q$ ) model.

Consider the following bivariate ( $k=2$ ) VARMA(1,1) model:

$\mb {y}_ t = \Phi \mb {y}_{t-1} + \bm {\epsilon }_ t - \Theta \bm {\epsilon }_{t-1}$

$\Phi =\left[\begin{matrix} 1.2 & -0.5 \cr 0.6 & 0.3 \cr \end{matrix}\right] ~ ~ \Theta =\left[\begin{matrix} -0.6 & 0.3 \cr 0.3 & 0.6 \cr \end{matrix} \right] ~ ~ \Sigma =\left[\begin{matrix} 1.0 & 0.5 \cr 0.5 & 1.25 \cr \end{matrix}\right]$

To compute the cross-covariance matrices of this model, you can use the following statements:

phi  = { 1.2 -0.5, 0.6 0.3 };
theta= {-0.6  0.3, 0.3 0.6 };
sigma= { 1.0  0.5, 0.5 1.25};
call varmacov(cov, phi, theta, sigma) lag=3;
Lag = {"0", "", "1", "", "2", "", "3", ""};
print Lag cov;

Figure 24.423: Cross-Covariance Matrix

Lag	cov
0	12.403036	8.4702334
	8.4702334	9.0377769
1	11.098527	9.3828916
	5.5703916	6.8934731
2	8.626786	9.4739834
	3.2377334	5.4102769
3	5.6151515	8.0182666
	1.1801416	3.5657231