TRISOLV Function :: SAS/IML(R) 13.1 User's Guide

TRISOLV Function

TRISOLV (form, R, b <, piv> ) ;

The TRISOLV function efficiently solves linear systems that involve a triangular matrix.

The TRISOLV function returns the $n \times p$ matrix $\mathbf{X}$ that contains $p$ solutions of the $p$ linear systems specified by form, R, and b.

The arguments to the TRISOLV function are as follows:

form

specifies which of the following form of a triangular linear system is to be solved:

form=1: solve 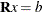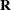$\mathbf{R} x = b$ , $\mathbf{R}$ upper triangular
form=2: solve 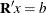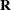$\mathbf{R}^{\prime } x = b$ , $\mathbf{R}$ upper triangular
form=3: solve 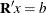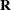$\mathbf{R}^{\prime } x = b$ , $\mathbf{R}$ lower triangular
form=4: solve 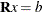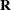$\mathbf{R} x = b$ , $\mathbf{R}$ lower triangular

R

specifies the 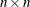$n \times n$ nonsingular upper (form=1,2) or lower (form=3,4) triangular coefficient matrix 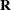$\mathbf{R}$ . Only the upper or lower triangle of argument matrix R is used; the other triangle can contain any information.

b

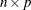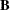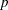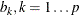specifies the $n \times p$ matrix, $\mathbf{B}$ , of $p$ right-hand sides $b_ k, k=1 \ldots p$ .

piv

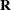specifies an optional $n$ vector that relates the order of the columns of matrix $\mathbf{R}$ to the order of the columns of an original coefficient matrix 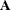$\mathbf{A}$ for which matrix 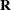$\mathbf{R}$ has been computed as a factor. For example, the vector piv can be the result of the QR decomposition of a matrix 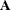$\mathbf{A}$ whose columns were permuted in the order $\mathbf{A}_{piv[1]}, \ldots , \mathbf{A}_{piv[n]}$ .

For form=1 and form=3, the solution is obtained by backward elimination. For form=2 and form=4, the solution is obtained by forward substitution.

If TRISOLV recognizes the upper or lower triangular matrix $\mathbf{R}$ as a singular matrix (that is, one that contains at least one zero diagonal element), it exits with an error message.

Consider the following example:

R = { 1  0  0  0,
      3  2  0  0,
      1 -3  5  0,
      2  7  9 -1 };

b = {1, 1, 4, -6 };
x = trisolv(4, R, b);
print x;

Figure 24.412: Solution of a Triangular System

x
1
-1
0
1

Also see the example in section The Full-Rank Linear Least Squares Problem.