SUB2NDX Function :: SAS/IML(R) 13.1 User's Guide

SUB2NDX Function

SUB2NDX (dim, subscripts ) ;

The SUB2NDX function is part of the IMLMLIB library. The SUB2NDX function module converts subscripts of a matrix into indices for the matrix. The arguments are as follows:

dim: specifies the dimensions of the matrix. For example, the value of this argument might be the 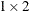$1\times 2$ vector that is returned from the DIMENSION function.
subscripts: is a matrix with 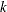$k$ columns that specifies the elements of a matrix. The first column of subscripts specifies the first subscript dimension, the second column specifies the second subscript dimension, and so forth. When 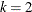$k=2$ , the first column of subscripts specifies the row subscripts and the second column specifies the column subscripts.

The SUB2NDX function converts subscripts to indices. For a two-dimensional matrix, subscripts are pairs $(i,j)$ such that $1\leq i \leq n$ and $1\leq j \leq p$ . The indices of an $n\times p$ matrix are the elements $1, 2, \ldots , np$ . The indices enumerate the elements in row-major order: the first $p$ indices enumerate the first row, the next $p$ indices enumerate the second row, and so forth.

The following statements construct a tridiagonal matrix that contains 2s on the diagonal and 1s on the sub- and superdiagonals. The DIAG function is used to construct a diagonal matrix. The subscripts of the superdiagonal (which, for this example, are (1,2), (2,3), and (3,4)) and the subdiagonal (which are (2,1), (3,2), and (4,3)) are then enumerated. The SUB2IND module converts these subscripts to indices, and the value 1 is assigned to all off-diagonal elements of the matrix.

/* construct a tridiagonal matrix */
y = diag({2,2,2,2}); /* assign diagonal */
p = ncol(y);
supDiag = T(1:p-1) || T(2:p); /* subscripts for superdiagonal */
subDiag = T(2:p) || T(1:p-1); /* subscripts for subdiagonal */
/* find index of all super- and subdiagonal elements */
dim = dimension(y);
idx = sub2ndx(dim, supDiag//subDiag);
y[idx] = 1; /* assign sub- and superdiagonal to 1 */
print y;

Figure 24.397: Subscripts That Correspond to Indices

y
2	1	0	0
1	2	1	0
0	1	2	1
0	0	1	2

You can also use the SUB2NDX function to store the results of a multidimensional array in a matrix. For an array with $d$ dimensions, a subscript is a $d$ -dimensional vector $(i_1, i_2,\ldots ,i_ k)$ , where $1\leq i_ j \leq d_ j$ for $j=1 \ldots k$ . For example, suppose you store the values of a $4 \times 3 \times 3$ array in a $12 \times 3$ matrix. The following program computes the indices that correspond to the first, middle, and last elements in the matrix:

dim = {4 3 3};/* a 12x3 matrix can store values from 4x3x3 array */
s = {1 1 1,
     2 3 3,
     4 3 3};
ndx = sub2ndx(dim, s);
print ndx;