PV Function :: SAS/IML(R) 13.1 User's Guide

PV Function

PV (times,flows,freq,rates) ;

The PV function returns a scalar that contains the present value of the cash flows based on the specified frequency and rates.

The arguments to the function are as follows:

times: is an 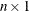$n \times 1$ column vector of times. Elements should be nonnegative.
flows: is an 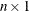$n \times 1$ column vector of cash flows.
freq: is a scalar that represents the base of the rates to be used for discounting the cash flows. If positive, it represents discrete compounding as the reciprocal of the number of compoundings per period. If zero, it represents continuous compounding. If –1, the rates represent per-period discount factors. No other negative values are accepted.
rates: is an 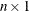$n \times 1$ column vector of rates to be used for discounting the cash flows. Elements should be positive.

A general present value relationship can be written as

$\begin{equation*} P=\sum _{k=1}^{K} c(k) D(t_ k) \end{equation*}$

where $P$ is the present value of the asset, $\{ c(k)\} , k=1,\ldots ,K$ , is the sequence of cash flows from the asset, $t_ k$ is the time to the $k$ th cash flow in periods from the present, and $D(t)$ is the discount function for time $t$ . The discount factors are as follows:

with per-unit-time-period discount factors $d_ t$ :

$\begin{equation*} D(t) = d_ t^ t \end{equation*}$
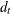with continuous compounding:

$\begin{equation*} D(t) = e^{-r_ t t} \end{equation*}$
with discrete compounding:

$\begin{equation*} D(t) = (1+fr)^{-t/f} \end{equation*}$

where $f > 0$ is the frequency, the reciprocal of the number of compoundings per unit time period.

The following statements present an example of using the PV function in the DATA step:

data a;
  pv = mort(., 438.79, 0.10/12, 30*12);
run;
proc print data=a; run;

Figure 24.278: Present Value Computation (DATA Step)

OBS	pv
1	50000.48

You can do the same computation by using the PV function in SAS/IML software. The first example uses a monthly rate; the second example uses an annual rate.

proc iml;
/*  If rate is specified as annual rate divided by 12 and FREQ=1,
 *  then results are equal to those computed by the MORT function. */
timesn = t(1:360);
flows = repeat(438.79, 360);
rate = repeat(0.10/12, 360);
freq = 1;
pv = pv(timesn, flows, freq, rate);
print pv;

/*  If rate is specified as annual rate, then the cash flow TIMES
 *  need to be specified in 1/12 increments and the FREQ=1/12.
 *  This produces the same result as the previous PV call. */
timesn = t(do(1/12, 30, 1/12));
flows = repeat(438.79, 360);
rate = repeat(0.10, 360); /* specify annual rate  */
freq = 1/12;              /* 12 compoundings annually */
pv = pv(timesn, flows, freq, rate);
print pv;

Figure 24.279: Present Value Computation (PROC IML)

pv
50000.48

pv
50000.48