PRODUCT Function :: SAS/IML(R) 13.1 User's Guide

PRODUCT Function

PRODUCT (a, b <, dim> ) ;

The PRODUCT function multiplies matrices of polynomials.

The arguments to the PRODUCT function are as follows:

a: is an 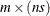$m \times (ns)$ numeric matrix. The first $m \times n$ submatrix contains the constant terms of the polynomials, the second $m \times n$ submatrix contains the first-order terms, and so on.
b: is an 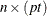$n \times (pt)$ matrix. The first 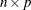$n \times p$ submatrix contains the constant terms of the polynomials, the second 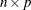$n \times p$ submatrix contains the first-order terms, and so on.
dim: is a 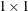$1 \times 1$ matrix, with value 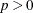$p>0$ . The value of this matrix is used to set the dimension 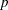$p$ of the matrix 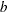$b$ . If omitted, the value of 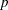$p$ is set to 1.

The PRODUCT function multiplies matrices of polynomials. The value returned is the $m \times (p(s+t-1))$ matrix of the polynomial products. The first $m \times p$ submatrix contains the constant terms, the second $m \times p$ submatrix contains the first-order terms, and so on.

The PRODUCT function can be used to multiply the matrix operators employed in a multivariate time series model of the form

$\begin{equation*} \Phi _1(B) \Phi _2(B) \mb {Y}_ t = \Theta _1(B) \Theta _2(B) \epsilon _ t \end{equation*}$

where $\Phi _1(B)$ , $\Phi _2(B)$ , $\Theta _1(B)$ , and $\Theta _2(B)$ are matrix polynomial operators whose first matrix coefficients are identity matrices. Often $\Phi _2(B)$ and $\Theta _2(B)$ represent seasonal components that are isolated in the modeling process but multiplied with the other operators when forming predictors or estimating parameters. The RATIO function is often employed in a time series context as well.

For example, the following statements demonstrate the PRODUCT function:

m1 = {1 2 3 4,
      5 6 7 8};
m2 = {1 2 3,
      4 5 6};
r = product(m1, m2, 1);
print r;

Figure 24.275: A Product of Matrices of Polynomials

r
9	31	41	33
29	79	105	69