The OPSCAL function rescales qualitative data to be a least squares fit to quantitative data.
The arguments to the OPSCAL function are as follows:
- mlevel
-
specifies a scalar that has one of two values. When mlevel is 1, the qualit matrix is at the nominal measurement level; when mlevel is 2, it is at the ordinal measurement level.
- quanti
-
specifies an
 matrix of quantitative information assumed to be at the interval level of measurement.
matrix of quantitative information assumed to be at the interval level of measurement.
- qualit
-
specifies an
 matrix of qualitative information whose level of measurement is specified by mlevel. When qualit is omitted, mlevel must be 2 and a temporary qualit is constructed that contains the integers from 1 to
matrix of qualitative information whose level of measurement is specified by mlevel. When qualit is omitted, mlevel must be 2 and a temporary qualit is constructed that contains the integers from 1 to  in the first row, from
in the first row, from 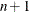 to
to 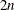 in the second row, from
in the second row, from 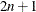 to
to 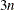 in the third row, and so forth, up to the integers
in the third row, and so forth, up to the integers 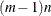 to
to 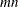 in the last(
in the last(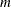 th) row. You cannot specify qualit as a character matrix.
th) row. You cannot specify qualit as a character matrix.
The result of the OPSCAL function is the optimal scaling transformation of the qualitative (nominal or ordinal) data in qualit. The optimal scaling transformation that results has the following properties:
-
It is a least squares fit to the quantitative data in quanti.
-
It preserves the qualitative measurement level of qualit.
When qualit is at the nominal level of measurement, the optimal scaling transformation result is a least squares fit to quanti, given the restriction that the category structure of qualit must be preserved. If element ![]() of qualit is in category
of qualit is in category ![]() , then element
, then element ![]() of the optimum scaling transformation result is the mean of all those elements of quanti that correspond to elements of qualit that are in category
of the optimum scaling transformation result is the mean of all those elements of quanti that correspond to elements of qualit that are in category ![]() .
.
For example, the following statements create the vector shown in Figure 24.255:
quanti = {5 4 6 7 4 6 2 4 8 6};
qualit = {6 6 2 12 4 10 4 10 8 6};
os = opscal(1, quanti, qualit);
print os;
Figure 24.255: Optimal Scaling Transformation of Nominal Data
| os | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| COL1 | COL2 | COL3 | COL4 | COL5 | COL6 | COL7 | COL8 | COL9 | COL10 | |
| ROW1 | 5 | 5 | 6 | 7 | 3 | 5 | 3 | 5 | 8 | 5 |
The optimal scaling transformation result is said to preserve the nominal measurement level of qualit because wherever there was a qualit category ![]() , there is now a result category label
, there is now a result category label ![]() . The transformation is least squares because the result element
. The transformation is least squares because the result element ![]() is the mean of appropriate elements of quanti. This is Young’s (1981) discrete-nominal transformation.
is the mean of appropriate elements of quanti. This is Young’s (1981) discrete-nominal transformation.
When qualit is at the ordinal level of measurement, the optimal scaling transformation result is a least squares fit to quanti, given the restriction that the ordinal structure of qualit must be preserved. This is done by determining blocks of elements of qualit so that if element ![]() of qualit is in block
of qualit is in block ![]() , then element
, then element ![]() of the result is the mean of all those quanti elements that correspond to block
of the result is the mean of all those quanti elements that correspond to block ![]() elements of qualit so that the means are (weakly) in the same order as the elements of qualit.
elements of qualit so that the means are (weakly) in the same order as the elements of qualit.
For example, consider these statements, which produce the transformation shown in Figure 24.256:
os2 = opscal(2, quanti, qualit); print os2;
Figure 24.256: Optimal Scaling Transformation of Ordinal Data
| os2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| COL1 | COL2 | COL3 | COL4 | COL5 | COL6 | COL7 | COL8 | COL9 | COL10 | |
| ROW1 | 5 | 5 | 4 | 7 | 4 | 6 | 4 | 6 | 6 | 5 |
This transformation preserves the ordinal measurement level of qualit because the elements of qualit and the result are (weakly) in the same order. It is least squares because the result elements are the means of appropriate elements of quanti. By comparing this result to the nominal one, you see that categories whose means are incorrectly ordered have been merged together to form correctly ordered blocks. This is known as Kruskal’s (1964) least squares monotonic transformation.
You can omit the qualit argument, as shown in the following statements:
quanti = {5 3 6 7 5 7 8 6 7 8};
os3 = opscal(2, quanti);
print os3;
These statements are equivalent to specifying
qualit = 1:10;
The result is shown in Figure 24.257.
Figure 24.257: Optimal Scaling Transformation
| os3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| COL1 | COL2 | COL3 | COL4 | COL5 | COL6 | COL7 | COL8 | COL9 | COL10 | |
| ROW1 | 4 | 4 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 8 |