matrix1 >< matrix2 ;
matrix1 >< scalar ;
matrix1 >< vector ;
The element minimum operator (><) compares each element of matrix1 with the corresponding element of matrix2. The two matrices must be conformable. The operator computes a new matrix that contains the smaller of the two values that are being compared.
-
If either argument is a scalar, then an elementwise comparison is performed between each element of the matrix and the scalar.
-
You can also compare a matrix with a row or column vector, in which case the comparison is performed between the vector and each row or column of the
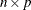matrix.
-
If you compare with an
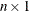column vector, each row of the matrix is compared with the corresponding row of the vector.
-
If you compare with a
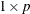row vector, each column of the matrix is compared with the corresponding column of the vector.
-
If a numeric missing value occurs in a matrix, the operator treats it as a value that is less than any valid nonmissing value.
The element minimum operator can take as operands two character matrices or a character matrix and a character string. Character values are compared in ASCII order. In ASCII order, numerals precede uppercase letters, which precede lowercase letters. If the element lengths of character operands are different, the shorter elements are padded on the right with blanks. The element length of the result is the longer of the two operand element lengths.
For example, the following statements compute the matrix c, shown in Figure 24.11:
a = { 2 4 6,
10 11 12};
b = { 1 9 2,
20 10 40};
c = a><b;
print c;