RANDNORMAL Function :: SAS/IML(R) 12.3 User's Guide

RANDNORMAL Function

RANDNORMAL (N, Mean, Cov ) ;

The RANDNORMAL function returns an $N \times p$ matrix that contains random draws from the multivariate normal distribution with mean vector Mean and covariance matrix Cov.

The inputs are as follows:

N: is the number of desired observations sampled from the multivariate normal distribution.
Mean: is a $1 \times p$ vector of means.
Cov: is a $p \times p$ symmetric positive definite variance-covariance matrix.

If follows a multivariate normal distribution with mean vector $\mu$ and variance-covariance matrix $\Sigma$ , then

the probability density function for is

$f(x; \mu , \Sigma ) = \frac{1}{(2 \pi )^{p/2} |\Sigma |^{1/2}} \exp \left( - \frac{(x-\mu ) \Sigma ^{-1} (x-\mu )^ T}{2} \right)$
if , the probability density function reduces to a univariate normal distribution.
the expected value of is $\mu _ i$ .
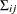the covariance of and is $\Sigma _{ij}$ .

The following example generates 1,000 samples from a two-dimensional multivariate normal distribution with mean vector $(1 \, 2)$ and a given covariance matrix. Each row of the returned matrix x is a row vector sampled from the multivariate normal distribution. The example computes the sample mean and covariance and compares them with the expected values.

call randseed(1);
N = 1000;
Mean = {1 2};
Cov = {2.4 3, 3 8.1};

x = RandNormal( N, Mean, Cov );
SampleMean = x[:,]; 
y = x - SampleMean;
SampleCov = y`*y / (N-1);
print SampleMean Mean, SampleCov Cov;

Figure 24.12: Estimated Mean and Covariance Matrix

SampleMean		Mean
1.0619604	2.1156084	1	2

SampleCov		Cov
2.5513518	3.2729559	2.4	3
3.2729559	8.7099585	3	8.1

For further details about sampling from the multivariate normal distribution, see Gentle (2003).