The MDC Procedure

As discussed under multinomial and conditional logits, the odds ratios in the multinomial or conditional logits are independent of the other alternatives. See the section Multinomial Logit and Conditional Logit. This property of the logit models is often viewed as rather restrictive and provides substitution patterns that do not represent the actual relationship among choice alternatives.

This independence assumption, called independence of irrelevant alternatives (IIA), can be tested with Hausman’s specification test. According to Hausman and McFadden (1984), if a subset of choice alternatives is irrelevant, it can be omitted from the sample without changing the remaining parameters systematically.

Under the null hypothesis (IIA holds), omitting the irrelevant alternatives leads to consistent and efficient parameter estimates 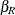, while parameter estimates from the unrestricted model are consistent but inefficient. Under the alternative, only the parameter estimates obtained from the unrestricted model are consistent.

This example demonstrates the use of Hausman’s specification test to analyze the IIA assumption and decide on an appropriate model that provides less restrictive substitution patterns (nested logit or multinomial probit). A sample data set of 527 automobile commuters in the San Francisco Bay Area is used (Small 1982). The regular time of arrival is recorded as between 42.5 minutes early and 17.5 minutes late, and is indexed by 12 alternatives, using five-minute interval groups. See Small (1982) for more details about these data.

The data can be divided into three groups: commuters who arrive early (alternatives 1 – 8), commuters who arrive on time (alternative 9), and commuters who arrive late (alternatives 10 – 12). Suppose that you want to test whether the IIA assumption holds for commuters who arrived on time (alternative 9).

Hausman’s specification test is distributed as 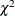with k degrees of freedom (equal to the number of independent variables) and can be written as

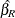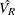where and represent parameter estimates and the variance-covariance matrix, respectively, from the model where the ninth alternative was omitted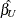, and and 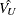represent parameter estimates and the variance-covariance matrix, respectively, from the full model. The following macro can be used to perform the IIA test for the ninth alternative:

/*---------------------------------------------------------------
 * name: %IIA
 * note: This macro test the IIA hypothesis using the Hausman's
 *       specification test. Inputs into the macro are as follows:
 *       indata:    input data set
 *       varlist:   list of RHS variables
 *       nchoice:   number of choices for each individual
 *       choice:    list of choices
 *       nvar:      number of independent variables
 *       nIIA:      number of choice alternatives used to test IIA
 *       IIA:       choice alternatives used to test IIA
 *       id:        ID variable
 *       decision:  0-1 LHS variable representing nchoice choices
 * purpose: Hausman's specification test
 *--------------------------------------------------------------*/

%macro IIA(indata=, varlist=, nchoice=, choice= , nvar= , IIA= ,
               nIIA=, id= , decision=);

   %let n=%eval(&nchoice-&nIIA);

   proc mdc data=&indata outest=cov covout ;
      model &decision = &varlist /
               type=clogit
               nchoice=&nchoice;
      id &id;
   run;

   data two;
      set &indata;
      if &choice in &IIA and &decision=1 then output;
   run;

   data two;
      set two;
      keep &id ind;
      ind=1;
   run;

   data merged;
      merge &indata two;
      by &id;
      if ind=1 or &choice in &IIA then delete;
   run;

   proc mdc data=merged outest=cov2 covout ;
      model &decision = &varlist /
               type=clogit
               nchoice=&n;
      id &id;
   run;

   proc IML;
      use cov var{_TYPE_ &varlist};
         read first into BetaU;
         read all into CovVarU where(_TYPE_='COV');
      close cov;

      use cov2 var{_TYPE_ &varlist};
         read first into BetaR;
         read all into CovVarR where(_TYPE_='COV');
      close cov;

      tmp = BetaU-BetaR;
      ChiSq=tmp*ginv(CovVarR-CovVarU)*tmp`;
      if ChiSq<0 then ChiSq=0;
      Prob=1-Probchi(ChiSq, &nvar);
      Print "Hausman Test for IIA for Variable &IIA";
      Print ChiSq Prob;
   run; quit;

%mend IIA;

The following statement invokes the %IIA macro to test IIA for commuters who arrive on time:

%IIA( indata=small,
      varlist=r15 r10 ttime ttime_cp sde sde_cp sdl sdlx d2l,
      nchoice=12,
      choice=alt,
      nvar=9,
      nIIA=1,
      IIA=(9),
      id=id,
      decision=decision );

The obtained 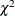of 7.9 and the p-value of 0.54 indicate that IIA holds for commuters who arrive on time (alternative 9). If the IIA assumption did not hold, the following model (nested logit), which reserves a subcategory for alternative 9, might be more appropriate. See Figure 25.30.

proc mdc data=small maxit=200 outest=a;
   model decision = r15 r10 ttime ttime_cp sde sde_cp
                    sdl sdlx d2l /
            type=nlogit
            choice=(alt);
   id id;
   utility u(1, ) = r15 r10 ttime ttime_cp sde sde_cp
                    sdl sdlx d2l;
   nest level(1) = (1 2 3 4 5 6 7 8 @ 1, 9 @ 2, 10 11 12 @ 3),
        level(2) = (1 2 3 @ 1);
run;

Similarly, IIA could be tested for commuters who arrive approximately on time (alternative 8, 9, 10), as follows:

%IIA( indata=small,
      varlist=r15 r10 ttime ttime_cp sde sde_cp sdl sdlx d2l,
      nchoice=12,
      choice=alt,
      nvar=9,
      nIIA=3,
      IIA=(8 9 10),
      id=id,
      decision=decision );

Based on this test, independence of irrelevant alternatives is not rejected for this subgroup (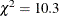 and p-value=0.326), and it is concluded that a more complex nested logit model with commuters who arrive approximately on time in one subcategory is not needed. Since the two Hausman’s specification tests just performed did not reject IIA, it might be a good idea to test whether the nested logit model is even needed. This is done using the likelihood ratio test in the next example.