The MDC Procedure

Model Fit and Goodness-of-Fit Statistics

McFadden (1974) suggests a likelihood ratio index that is analogous to the R-square in the linear regression model:

\[ R^{2}_{M} = 1 - \frac{\ln L}{\ln L_{0}} \]

where L is the maximum of the log-likelihood function and 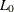$L_{0}$ is the maximum of the log-likelihood function when all coefficients, except for an intercept term, are zero. McFadden’s likelihood ratio index is bounded by 0 and 1.

Estrella (1998) proposes the following requirements for a goodness-of-fit measure to be desirable in discrete choice modeling:

  • The measure must take values in $[0,1]$, where 0 represents no fit and 1 corresponds to perfect fit.

  • The measure should be directly related to the valid test statistic for the significance of all slope coefficients.

  • The derivative of the measure with respect to the test statistic should comply with corresponding derivatives in a linear regression.

Estrella’s measure is written as

\[ R_{E1}^{2} = 1 - \left(\frac{\ln L}{\ln L_{0}}\right) ^{-(2 / N) \ln L_{0}} \]

Estrella suggests an alternative measure,

\[ R_{E2}^{2} = 1 - [ (\ln L - K) / \ln L_{0} ]^{-(2 / N) \ln L_{0}} \]

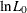where $\ln L_{0}$ is computed with null parameter values, N is the number of observations used, and K represents the number of estimated parameters.

Other goodness-of-fit measures are summarized as follows:

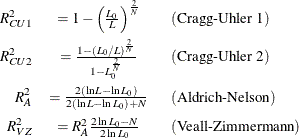
\begin{eqnarray*} R_{CU1}^{2} & = 1 - \left(\frac{L_{0}}{L}\right)^{\frac{2}{N}} \; \; & (\textrm{Cragg-Uhler 1}) \\ R_{CU2}^{2} & = \frac{1 - (L_{0}/L)^{\frac{2}{N}}}{1 - L_{0}^{\frac{2}{N}}} \; \; & (\textrm{Cragg-Uhler 2}) \\ R_{A}^{2} & = \frac{2(\ln L - \ln L_{0})}{2(\ln L - \ln L_{0})+N} \; \; & (\textrm{Aldrich-Nelson}) \\ R_{VZ}^{2} & = R_{A}^{2}\frac{2\ln L_{0} - N}{2\ln L_{0}} \; \; & (\textrm{Veall-Zimmermann}) \end{eqnarray*}

The AIC and SBC are computed as follows:

\[ AIC = -2\; ln(L)+2\; k \]
\[ SBC = -2\; ln(L)+ln(n)\; k \]

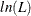where $ln(L)$ is the log-likelihood value for the model, k is the number of parameters estimated, and n is the number of observations (that is, the number of respondents).