SAS Macros and Functions

LOGTEST Macro

Subsections:

The %LOGTEST macro tests whether a logarithmic transformation is appropriate for modeling and forecasting a time series. The logarithmic transformation is often used for time series that show exponential growth or variability proportional to the level of the series.

The %LOGTEST macro fits an autoregressive model to a series and fits the same model to the log of the series. Both models are estimated by the maximum-likelihood method, and the maximum log-likelihood values for both autoregressive models are computed. These log-likelihood values are then expressed in terms of the original data and compared.

You can control the order of the autoregressive models. You can also difference the series and the log-transformed series before the autoregressive model is fit.

You can print the log-likelihood values and related statistics (AIC, SBC, and MSE) for the autoregressive models for the series and the log-transformed series. You can also output these statistics to a SAS data set.

Syntax

The %LOGTEST macro has the following form:

  • %LOGTEST ( SAS-data-set, variable, < options > );

The first argument, SAS-data-set, specifies the name of the SAS data set that contains the time series variable to be analyzed. The second argument, variable, specifies the time series variable name to be analyzed.

The first two arguments are required. The following options can be used with the %LOGTEST macro. Options must follow the required arguments and are separated by commas.

AR=n

specifies the order of the autoregressive model fit to the series and the log-transformed series. The default is AR=5.

CONST=value

specifies a constant to be added to the series before transformation. Use the CONST= option when some values of the series are 0 or negative. The series analyzed must be greater than the negative of the CONST= value. The default is CONST=0.

DIF=( differencing-list )

specifies the degrees of differencing applied to the original and log-transformed series before fitting the autoregressive model. The differencing-list is a list of positive integers separated by commas and enclosed in parentheses. For example, DIF=(1,12) specifies that the transformed series be differenced once at lag 1 and once at lag 12. For more details, see the section IDENTIFY Statement in Chapter 8: The ARIMA Procedure.

OUT=SAS-data-set

writes the results to an output data set. The output data set includes a variable TRANS that identifies the transformation (LOG or NONE), the log-likelihood value (LOGLIK), residual mean squared error (RMSE), Akaike Information Criterion (AIC), and Schwarz’s Bayesian Criterion (SBC) for the log-transformed and untransformed cases.

PRINT=YES | NO

specifies whether the results are printed. The default is PRINT=NO. The printed output shows the log-likelihood value, residual mean squared error, Akaike Information Criterion (AIC), and Schwarz’s Bayesian Criterion (SBC) for the log-transformed and untransformed cases.

Results

The result of the test is returned in the macro variable &LOGTEST. The value of the &LOGTEST variable is ‘LOG’ if the model fit to the log-transformed data has a larger log likelihood than the model fit to the untransformed series. The value of the &LOGTEST variable is ‘NONE’ if the model fit to the untransformed data has a larger log likelihood. The variable &LOGTEST is set to ‘ERROR’ if the %LOGTEST macro is unable to compute the test due to errors.

Results are printed when the PRINT=YES option is specified. Results are stored in SAS data sets when the OUT= option is specified.

Details

Assume that a time series 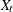${X_{t}}$ is a stationary pth order autoregressive process with normally distributed white noise innovations. That is,

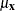\[ (1 - {\Theta }({B}) ) (X_{t}-{\mu }_{\mb{x} }) = {\epsilon }_{t} \]

where ${\mu }_{\mb{x} }$ is the mean of ${X_{t}}$.

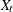The log likelihood function of 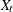${X_{t}}$ is

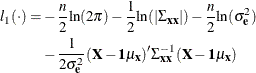
\begin{equation*} \begin{split} l_{1}({\cdot }) = & - \frac{n}{2} {\ln }(2{\pi }) - \frac{1}{2} {\ln }(|{\Sigma }_{\Strong{xx} }|) - \frac{n}{2} {\ln }( {\sigma }^{2}_{\Strong{e} }) \\ & - \frac{1}{2 {\sigma }^{2}_{\Strong{e} }} (\Strong{X} -\Strong{1} {\mu }_{\Strong{x} })’ {\Sigma }^{-1}_{\Strong{xx} }(\Strong{X} -\Strong{1} {\mu }_{\Strong{x} }) \end{split}\end{equation*}

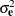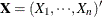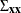where n is the number of observations, 1 is the n-dimensional column vector of 1s, ${\sigma }^{2}_{\mb{e} }$ is the variance of the white noise, ${\mb{X} =(X_{1},{\cdots }, X_{n})’}$, and ${{\Sigma }_{\mb{xx} }}$ is the covariance matrix of ${\mb{X} }$.

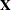On the other hand, if the log-transformed time series 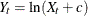${Y_{t} = {\ln }(X_{t}+c)}$ is a stationary pth order autoregressive process, the log-likelihood function of ${X_{t}}$ is

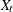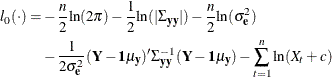
\begin{equation*} \begin{split} l_{0}({\cdot }) = & - \frac{n}{2} {\ln }(2{\pi }) - \frac{1}{2} {\ln }(|{\Sigma }_{\Strong{yy} }|) - \frac{n}{2} {\ln }( {\sigma }^{2}_{\Strong{e} }) \\ & - \frac{1}{2 {\sigma }^{2}_{\Strong{e} }} (\Strong{Y} -\Strong{1} {\mu }_{\Strong{y} })’ {\Sigma }^{-1}_{\Strong{yy} }(\Strong{Y} -\Strong{1} {\mu }_{\Strong{y} }) - \sum _{t=1}^{n}{{\ln }(X_{t}+c)} \end{split}\end{equation*}

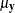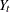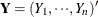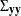where ${{\mu }_{\mb{y} }}$ is the mean of ${Y_{t}}$, ${\mb{Y} =(Y_{1},{\cdots },Y_{n})’}$, and ${{\Sigma }_{\mb{yy} }}$ is the covariance matrix of ${\mb{Y} }$.

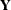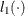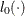The %LOGTEST macro compares the maximum values of ${l_{1}({\cdot })}$ and ${l_{0}({\cdot })}$ and determines which is larger.

The %LOGTEST macro also computes the Akaike Information Criterion (AIC), Schwarz’s Bayesian Criterion (SBC), and residual mean squared error based on the maximum likelihood estimator for the autoregressive model. For the mean squared error, retransformation of forecasts is based on Pankratz (1983, pp. 256–258).

After differencing as specified by the DIF= option, the process is assumed to be a stationary autoregressive process. You might want to check for stationarity of the series using the %DFTEST macro. If the process is not stationary, differencing with the DIF= option is recommended. For a process with moving average terms, a large value for the AR= option might be appropriate.