Options for Defining the Model and Controlling Diagnostic Statistics

The following options are used to define the model to be estimated and to control the output that is printed.

ALTPARM

specifies the alternative parameterization of the overall scale of transfer functions in the model. See the section Alternative Model Parameterization for details.

INPUT=variable

INPUT=( transfer-function variable ...)

specifies input variables and their transfer functions.

The variables used on the INPUT= option must be included in the CROSSCORR= list in the previous IDENTIFY statement. If any differencing is specified in the CROSSCORR= list, then the differenced series is used as the input to the transfer function.

The transfer function specification for an input variable is optional. If no transfer function is specified, the input variable enters the model as a simple regressor. If specified, the transfer function specification has the following syntax:

Here, S is a shift or lag of the input variable, the terms before the slash (/) are numerator factors, and the terms after the slash (/) are denominator factors of the transfer function. All three parts are optional. See the section Specifying Inputs and Transfer Functions for details.

METHOD=value

specifies the estimation method to use. METHOD=ML specifies the maximum likelihood method. METHOD=ULS specifies the unconditional least squares method. METHOD=CLS specifies the conditional least squares method. METHOD=CLS is the default. See the section Estimation Details for more information.

NOCONSTANT

NOINT

suppresses the fitting of a constant (or intercept) parameter in the model. (That is, the parameter 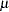is omitted.)

NODF

estimates the variance by dividing the error sum of squares (SSE) by the number of residuals. The default is to divide the SSE by the number of residuals minus the number of free parameters in the model.

NOPRINT

suppresses the normal printout generated by the ESTIMATE statement. If the NOPRINT option is specified for the ESTIMATE statement, then any error and warning messages are printed to the SAS log.

P=order

P=(lag, ..., lag ) ...(lag, ..., lag )

specifies the autoregressive part of the model. By default, no autoregressive parameters are fit.

P=(l , l , ..., l ) defines a model with autoregressive parameters at the specified lags. P= order is equivalent to P=(1, 2, ..., order).

A concatenation of parenthesized lists specifies a factored model. For example, P=(1,2,5)(6,12) specifies the autoregressive model

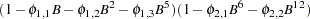
PLOT

plots the residual autocorrelation functions. The sample autocorrelation, the sample inverse autocorrelation, and the sample partial autocorrelation functions of the model residuals are plotted.

Q=order

Q=(lag, ..., lag ) ...(lag, ..., lag )

specifies the moving-average part of the model. By default, no moving-average part is included in the model.

Q=(l , l , ..., l ) defines a model with moving-average parameters at the specified lags. Q= order is equivalent to Q=(1, 2, ..., order). A concatenation of parenthesized lists specifies a factored model. The interpretation of factors and lags is the same as for the P= option.

WHITENOISE=ST | IGNOREMISS

specifies the type of test statistic that is used in the white noise test of the series when the series contains missing values. If WHITENOISE=IGNOREMISS, the standard Ljung-Box test statistic is used. If WHITENOISE=ST, a modification of this statistic suggested by Stoffer and Toloi (1992) is used. The default is WHITENOISE=ST.

Options for Output Data Sets

The following options are used to store results in SAS data sets:

OUTEST=SAS-data-set

writes the parameter estimates to an output data set. If the OUTCORR or OUTCOV option is used, the correlations or covariances of the estimates are also written to the OUTEST= data set. See the section OUTEST= Data Set for a description of the OUTEST= output data set.

OUTCORR

writes the correlations of the parameter estimates to the OUTEST= data set.

OUTCOV

writes the covariances of the parameter estimates to the OUTEST= data set.

OUTMODEL=SAS-data-set

writes the model and parameter estimates to an output data set. If OUTMODEL= is not specified, no model output data set is created. See the section OUTMODEL= SAS Data Set for a description of the OUTMODEL= output data set.

OUTSTAT=SAS-data-set

writes the model diagnostic statistics to an output data set. If OUTSTAT= is not specified, no statistics output data set is created. See the section OUTSTAT= Data Set for a description of the OUTSTAT= output data set.

Options to Specify Parameter Values

The following options enable you to specify values for the model parameters. These options can provide starting values for the estimation process, or you can specify fixed parameters for use in the FORECAST stage and suppress the estimation process with the NOEST option. By default, the ARIMA procedure finds initial parameter estimates and uses these estimates as starting values in the iterative estimation process.

If values for any parameters are specified, values for all parameters should be given. The number of values given must agree with the model specifications.

AR=value ...

lists starting values for the autoregressive parameters. See the section Initial Values for more information.

INITVAL=(initializer-spec variable ...)

specifies starting values for the parameters in the transfer function parts of the model. See the section Initial Values for more information.

MA=value ...

lists starting values for the moving-average parameters. See the section Initial Values for more information.

MU=value

specifies the MU parameter.

NOEST

uses the values specified with the AR=, MA=, INITVAL=, and MU= options as final parameter values. The estimation process is suppressed except for estimation of the residual variance. The specified parameter values are used directly by the next FORECAST statement. When NOEST is specified, standard errors, t values, and the correlations between estimates are displayed as 0 or missing. (The NOEST option is useful, for example, when you want to generate forecasts that correspond to a published model.)

Options to Control the Iterative Estimation Process

The following options can be used to control the iterative process of minimizing the error sum of squares or maximizing the log-likelihood function. These tuning options are not usually needed but can be useful if convergence problems arise.

BACKLIM=

omits the specified number of initial residuals from the sum of squares or likelihood function. Omitting values can be useful for suppressing transients in transfer function models that are sensitive to start-up values.

CONVERGE=value

specifies the convergence criterion. Convergence is assumed when the largest change in the estimate for any parameter is less that the CONVERGE= option value. If the absolute value of the parameter estimate is greater than 0.01, the relative change is used; otherwise, the absolute change in the estimate is used. The default is CONVERGE=0.001.

DELTA=value

specifies the perturbation value for computing numerical derivatives. The default is DELTA=0.001.

GRID

prints the error sum of squares (SSE) or concentrated log-likelihood surface in a small grid of the parameter space around the final estimates. For each pair of parameters, the SSE is printed for the nine parameter-value combinations formed by the grid, with a center at the final estimates and with spacing given by the GRIDVAL= specification. The GRID option can help you judge whether the estimates are truly at the optimum, since the estimation process does not always converge. For models with a large number of parameters, the GRID option produces voluminous output.

GRIDVAL=number

controls the spacing in the grid printed by the GRID option. The default is GRIDVAL=0.005.

MAXITER=

MAXIT=

specifies the maximum number of iterations allowed. The default is MAXITER=50.

NOLS

begins the maximum likelihood or unconditional least squares iterations from the preliminary estimates rather than from the conditional least squares estimates that are produced after four iterations. See the section Estimation Details for more information.

NOSTABLE

specifies that the autoregressive and moving-average parameter estimates for the noise part of the model not be restricted to the stationary and invertible regions, respectively. See the section Stationarity and Invertibility for more information.

PRINTALL

prints preliminary estimation results and the iterations in the final estimation process.

NOTFSTABLE

specifies that the parameter estimates for the denominator polynomial of the transfer function part of the model not be restricted to the stability region. See the section Stationarity and Invertibility for more information.

SINGULAR=value

specifies the criterion for checking singularity. If a pivot of a sweep operation is less than the SINGULAR= value, the matrix is deemed singular. Sweep operations are performed on the Jacobian matrix during final estimation and on the covariance matrix when preliminary estimates are obtained. The default is SINGULAR=1E–7.