The HPPANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names -
Example

- References
One-Way Fixed-Effects Model
The specification for the one-way fixed-effects model is
![\[ u_{it}={\gamma }_{i} + {\epsilon }_{it} \]](images/etshpug_hppanel0009.png)
where the 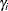 are nonrandom parameters to be estimated.
are nonrandom parameters to be estimated.
Let 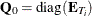 , with
, with 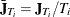 and
and 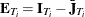 , where
, where 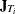 is a matrix of
is a matrix of 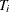 ones.
ones.
The matrix 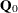 represents the within transformation. In the one-way model, the within transformation is the conversion of the raw data to
deviations from a cross section’s mean. The vector
represents the within transformation. In the one-way model, the within transformation is the conversion of the raw data to
deviations from a cross section’s mean. The vector 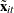 is a row of the general matrix
is a row of the general matrix 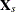 , where the subscripted s implies that the constant (column of ones) is missing.
, where the subscripted s implies that the constant (column of ones) is missing.
Let 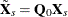 and
and 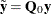 . The estimator of the slope coefficients is given by
. The estimator of the slope coefficients is given by
![\[ \tilde{{\beta }}_{s}=( \tilde{\mb{X} }^{'}_{s} \tilde{\mb{X} }_{s})^{-1} \tilde{\mb{X} }^{'}_{s}\tilde{\mb{y} } \]](images/etshpug_hppanel0021.png)
After the slope estimates have been calculated, the estimation of an intercept or the cross-sectional fixed effects is handled as follows. First, you obtain the cross-sectional effects:
![\[ \gamma _\mi {i} = \bar{\mi{y}}_\mi {i \cdot } - \tilde{{\beta }}_{s}\bar{\mb{\mi{x}}}_\mi {i \cdot } \quad \mbox{for}\quad \mi{i} = 1 \ldots \mi{N} \]](images/etshpug_hppanel0022.png)
If the NOINT option is specified, then the dummy variables’ coefficients are set equal to the fixed effects. If you want an intercept, then the ith dummy variable is obtained from the following expression:
![\[ D_\mi {i} = \gamma _\mi {i}- \gamma _\mi {N} \quad \mbox{for}\quad \mi{i} = 1 \ldots \mi{N} -1 \]](images/etshpug_hppanel0023.png)
The intercept is the Nth fixed effect 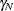 .
.
The within-model sum of squared errors is
![\[ \mr{SSE} = \sum _\mi {i = 1} ^\mi {N} \sum _\mi {t = 1} ^\mi {T_\mi {i}} (y_\mi {it} - \gamma _\mi {i} - \mb{X} _{s}\tilde{{\beta }}_{s})^{2} \]](images/etshpug_hppanel0025.png)
The estimated error variance can be written as
![\[ \hat{{\sigma }}_{{\epsilon }}^{2}= \mr{SSE} / (\mi{M}-\mi{N}-(\mi{K} -1)) \]](images/etshpug_hppanel0026.png)
Alternatively, an equivalent way to express the error variance is
![\[ \hat{{\sigma }}_{{\epsilon }}^{2}=\tilde{\mb{u} }^{'}\mb{Q} _{0} \tilde{\mb{u} } / (\mi{M}-\mi{N}-(\mi{K} -1)) \]](images/etshpug_hppanel0027.png)
where the residuals  are given by
are given by 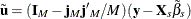 if there is an intercept and by
if there is an intercept and by 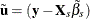 if there is not. The drawback is that the formula changes (but the results do not) with the inclusion of a constant.
if there is not. The drawback is that the formula changes (but the results do not) with the inclusion of a constant.
The variance covariance matrix of 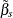 is given by
is given by
![\[ \mr{Var}\left[{\tilde{\beta }}_{s}\right] = \hat{{\sigma }}_{{\epsilon }}^{2}(\tilde{\mb{X} }^{'}_{s} \tilde{\mb{X} }_{s})^{-1} \]](images/etshpug_hppanel0032.png)
The covariance of the dummy variables and the dummy variables with the 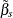 depends on whether the intercept is included in the model. For more information, see the section One-Way Fixed-Effects Model in SAS/ETS 14.1 User's Guide.
depends on whether the intercept is included in the model. For more information, see the section One-Way Fixed-Effects Model in SAS/ETS 14.1 User's Guide.
Alternatively, the FIXONETIME model option estimates a one-way model in which the heterogeneity comes from time effects. This option is analogous to re-sorting the data by time and then by cross section, and then running a FIXONE model. The advantage of using the FIXONETIME option is that sorting is avoided and the model remains labeled correctly.