Sample 59236: Fitting Zero-Inflated Count Data Models by Using PROC GENMOD
 |  |  |  |
Overview
Count data sometimes exhibit a greater proportion of zero counts than is consistent with the data having been generated by a simple Poisson or negative binomial process. For example, a preponderance of zero counts have been observed in data that record the number of automobile accidents per driver, the number of criminal acts per person, the number of derogatory credit reports per person, the number of incidences of a rare disease in a population, and the number of defects in a manufacturing process, just to name a few. Failure to properly account for the excess zeros constitutes a model misspecification that can result in biased or inconsistent estimators.
Zero-inflated count models provide one method to explain the excess zeros by modeling the data as a mixture of two separate distributions: one distribution is typically a Poisson or negative binomial distribution that can generate both zero and nonzero counts, and the second distribution is a constant distribution that generates only zero counts. When a zero count is observed, there is some probability, called the zero-inflation probability, that the observation came from the always-zero distribution; the probability that the zero came from the Poisson/negative binomial distribution is 1 minus the zero-inflation probabilty. When the underlying count distribution is a Poisson distribution, the mixture is called a zero-inflated Poisson (ZIP) distribution; when the underlying count distribution is a negative binomial distribution, the mixture is called a zero-inflated negative binomial (ZINB) distribution.
This example demonstrates how to fit both ZIP and ZINB models by using the GENMOD procedure.
Analysis
Count data that have an incidence of zeros greater than expected for the underlying probability distribution can be modeled with a zero-inflated distribution. The population is considered to consist of two subpopulations. Observations drawn from the first subpopulation are realizations of a random variable that typically has either a Poisson or negative binomial distribution, which might contain zeros. Observations drawn from the second subpopulation always provide a zero count.
Suppose the mean of the underlying Poisson or negative binomial distribution is ![]() and the probability of an observation being drawn from the constant distribution that always generates zeros is
and the probability of an observation being drawn from the constant distribution that always generates zeros is ![]() . The parameter
. The parameter ![]() is often called the zero-inflation probability.
is often called the zero-inflation probability.
The probability distribution of a zero-inflated Poisson random variable Y is given by
![]()
The mean and variance of Y for the zero-inflated Poisson are given by

The parameters ![]() and
and ![]() can be modeled as functions of linear predictors,
can be modeled as functions of linear predictors,
![]()
where ![]() is one of the binary link functions: logit, probit, or complementary log-log. The log link function is typically used for
is one of the binary link functions: logit, probit, or complementary log-log. The log link function is typically used for ![]() .
.
The excess zeros are a form of overdispersion. Fitting a zero-inflated Poisson model can account for the excess zeros, but there are also other sources of overdispersion that must be considered. If there are sources of overdispersion that cannot be attributed to the excess zeros, failure to account for them constitutes a model misspecification, which results in biased standard errors. In a ZIP model, the underlying Poisson distribution for the first subpopulation is assumed to have a variance that is equal to the distribution’s mean. If this is an invalid assumption, the data exhibit overdispersion (or underdispersion).
A useful diagnostic tool that can aid you in detecting overdispersion is the Pearson chi-square statistic. Pearson’s chi-square statistic is defined as
![]()
This statistic, under certain regularity conditions, has a limiting chi-square distribution, with degrees of freedom equal to the number of observations minus the number of parameters estimated. Comparing the computed Pearson chi-square statistic to an appropriate quantile of a chi-square distribution with ![]() degrees of freedom constitutes a test for overdispersion.
degrees of freedom constitutes a test for overdispersion.
If overdispersion is detected, the ZINB model often provides an adequate alternative. The probability distribution of a zero-inflated negative binomial random variable Y is given by
![]()
where ![]() is the negative binomial dispersion parameter.
is the negative binomial dispersion parameter.
The mean and variance of Y for the zero-inflated negative binomial are given by

Because the ZINB model assumes a negative binomial distribution for the first component of the mixture, it has a more flexible variance function. Thus it provides a means to account for overdispersion that is not due to the excess zeros. However, the negative binomial, and thus the ZINB model, achieves this additional flexibility at the cost of an additional parameter. Thus, if you fit a ZINB model when there is no overdispersion, the parameter estimates are less efficient compared to the more parsimonious ZIP model. If the ZINB model does not fully account for the overdispersion, more flexible mixture models can be considered.
Example: Trajan Data Set
Consider a horticultural experiment to study the number of roots produced by a certain species of apple tree. During the rooting period, all shoots were maintained under identical conditions, but the shoots themselves were cultured on media that contained four different concentration levels of the cytokinin 6-benzylaminopurine (BAP), in growth cabinets with an 8 or 16 hour photoperiod (Ridout, Hinde, and Demétrio, 1998). The objective is to assess the effect of both the photoperiod and the concentration levels of BAP on the number of roots produced.
The analysis begins with a graphical inspection of the data. The following DATA step reads the data and Table 1 summarizes the variables in the data set Trajan.
data Trajan; input roots shoot photoperiod bap; lshoot=log(shoot); datalines; 0 40 8 17.6 0 40 8 17.6 0 30 16 2.2 0 30 16 2.2 ... more lines ... 13 30 8 4.4 14 40 8 8.8 14 40 8 8.8 14 40 8 17.6 17 30 8 2.2 ;
Table 1: Trajan Data Set
|
Variable Name |
Description |
|---|---|
|
|
Number of roots |
|
|
Number of micropropogated shoots |
|
|
Natural logarithm of the number of shoots |
|
|
Eight- or 16-hour photoperiod |
|
|
Concentrations of the cytokinin 6-benzylaminopurine (BAP) |
The FREQ procedure is then used to produce plots of the marginal and conditional distributions of the response variable Roots.
ods graphics on; proc freq data=Trajan; table roots / plots(only)=freqplot(scale=percent); run;
Inspection of Figure 1 reveals a percentage of zero counts that is much larger than what you would expect to observe if the data were generated by simple Poisson or negative binomial processes.
Figure 1: Marginal Distribution of Response Variable Roots

The following SAS statements produce plots of the distribution of Roots conditional on Photoperiod:
proc sort data=Trajan out=Trajan; by photoperiod; run;
proc freq data=Trajan; table roots / plots(only)=freqplot(scale=percent); by photoperiod; run;
Figure 2: Distribution of Roots Conditional on Photoperiod
|
|
|
|
|
|
Figure 2 reveals that under the 8-hour photoperiod, almost all of the shoots produced roots. In fact, conditional on Photoperiod=8, the distribution appears consistent with the data having been generated by a simple Poisson or negative binomial process. However, under the 16-hour photoperiod, almost half of the shoots produced no roots. This provides compelling evidence that the data generating process is a mixture and that the probability of observing a zero count is conditional on the photoperiod.
The following SAS statements produce plots of the distribution of Roots conditional on BAP:
proc sort data=Trajan out=Trajan; by bap; run;
proc freq data=Trajan; table roots / plots(only)=freqplot(scale=percent); by bap; run;
Figure 3: Distribution of Roots Conditional on BAP
|
|
|
|
|
|
Figure 4:
|
|
|
|
|
|
Figure 3 reveals differences in the modes and the skew of the conditional distributions. It is reasonable to conclude that the expected value of Roots is a function of the level of BAP. However, there is little variation in the percentage of zero counts in these conditional distributions, suggesting that BAP is probably not a predictor of the probability of a zero count.
The following SAS statements produce plots of the distribution of Roots conditional on Photoperiod and BAP:
proc sort data=Trajan out=Trajan; by photoperiod bap; run;
proc freq data=Trajan; table roots / plots(only)=freqplot(scale=percent); by photoperiod bap; run;
Figure 5: Distribution of Roots Conditional on Photoperiod and BAP
|
|
|
|
|
|
Figure 6:
|
|
|
|
|
|
Figure 7:
|
|
|
|
|
|
Figure 8:
|
|
|
|
|
|
The conditional distributions in which Photoperiod = 8 reveal some differences in the modes and skew. The conditional distributions in which Photoperiod = 16 are dominated by the large percentages of zero counts. There is some indication of interaction effects, but it is difficult to predict whether they are significant.
To summarize, the graphical evidence indicates that a simple Poisson or negative binomial model will not likely account for the prevalence of zero counts and that a mixture model such as a zero-inflated Poisson (ZIP) model or zero-inflated negative binomial (ZINB) is needed. There is also clear evidence that the probability of a zero count depends on the level of Photoperiod.
The following SAS statements use the GENMOD procedure to fit a zero-inflated Poisson model to the response variable Roots.
proc genmod data=Trajan; class bap photoperiod; model roots = bap|photoperiod / dist=zip offset=lshoot; zeromodel photoperiod; output out=zip predicted=pred pzero=pzero; ods output Modelfit=fit; run;
The CLASS statement specifies that the variables Photoperiod and BAP are categorical variables. The MODEL statement includes Photoperiod, BAP, and their interactions in the model of the linear predictor. The DIST= option fits a zero-inflated Poisson model. The ZEROMODEL statement uses the default logit model to model the probability of a zero count and uses the variable Photoperiod as a linear predictor in the model. The OUTPUT statement saves the predicted values and the estimated conditional zero-inflation probabilities in the data set Zip. The predicted values and the zero-inflation probabilities are used later to generate graphical displays that help assess the model’s goodness-of-fit. The ODS OUTPUT statement saves the goodness-of-fit statistics to the data set Fit so that a formal test for overdispersion can be performed. If there is overdispersion, then the model is misspecified and the standard errors of the model parameters are biased downwards.
Output 1 displays the fit criteria for the ZIP model.
Output 1: ZIP Model of Roots Data
| Criteria For Assessing Goodness Of Fit | |||
|---|---|---|---|
| Criterion | DF | Value | Value/DF |
| Deviance | 1244.4566 | ||
| Scaled Deviance | 1244.4566 | ||
| Pearson Chi-Square | 260 | 330.6476 | 1.2717 |
| Scaled Pearson X2 | 260 | 330.6476 | 1.2717 |
| Log Likelihood | 1137.1695 | ||
| Full Log Likelihood | -622.2283 | ||
| AIC (smaller is better) | 1264.4566 | ||
| AICC (smaller is better) | 1265.3060 | ||
| BIC (smaller is better) | 1300.4408 | ||
Most of the criteria are useful only for comparing the model fit among given alternative models. However, the Pearson statistic can be used to determine if there is any evidence of overdispersion. If the model is correctly specified and there is no overdispersion, the Pearson chi-square statistic divided by the degrees-of-freedom has an expected value of 1. The obvious question is whether the observed value of 1.2717 is significantly different from 1, and thus an indication of overdispersion. As indicated in the section Analysis, the scaled Pearson statistic for generalized linear models has a limiting chi-square distribution under certain regularity conditions with degrees of freedom equal to the number of observations minus the number of estimated parameters. For Poisson and negative binomial models, the scale is fixed at 1, so there is no difference between the scaled and unscaled versions of the statistic. Therefore, a formal one-sided test for overdispersion is performed by computing the probability of observing a larger value of the statistic. The following SAS statements compute the p-value for such a test:
data fit; set fit(where=(criterion="Scaled Pearson X2")); format pvalue pvalue6.4; pvalue=1-probchi(value,df); run;
proc print data=fit noobs; var criterion value df pvalue; run;
Output 2 reveals a p-value of 0.002 indicating rejection of the null hypothesis of no overdispersion at the most commonly used confidence levels.
Output 2: Pearson Chi-Square Statistic
| Criterion | Value | DF | pvalue |
|---|---|---|---|
| Scaled Pearson X2 | 330.6476 | 260 | 0.0020 |
Output 3 presents the parameter estimates for the ZIP model. Because of the evidence of overdispersion, inferences based on these estimates are suspect; the standard errors are likely to be biased downwards. Nevertheless, the results as presented indicate that Photoperiod and BAP are significant determinants of the expected value, as are three of the four interactions. Also as expected, Photoperiod is a significant predictor of the probability of a zero count.
Output 3: ZIP Model Parameter Estimates
The GENMOD Procedure
The GENMOD Procedure
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |||
| Intercept | 1 | -2.1581 | 0.1033 | -2.3607 | -1.9556 | 436.14 | <.0001 | ||
| bap | 2.2 | 1 | 0.6322 | 0.1449 | 0.3483 | 0.9162 | 19.04 | <.0001 | |
| bap | 4.4 | 1 | 0.5209 | 0.1521 | 0.2228 | 0.8191 | 11.73 | 0.0006 | |
| bap | 8.8 | 1 | 0.4058 | 0.1468 | 0.1182 | 0.6935 | 7.65 | 0.0057 | |
| bap | 17.6 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . | |
| photoperiod | 8 | 1 | 0.4857 | 0.1193 | 0.2519 | 0.7195 | 16.58 | <.0001 | |
| photoperiod | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . | |
| bap*photoperiod | 2.2 | 8 | 1 | -0.5974 | 0.1739 | -0.9383 | -0.2565 | 11.80 | 0.0006 |
| bap*photoperiod | 2.2 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 4.4 | 8 | 1 | -0.1998 | 0.1760 | -0.5448 | 0.1451 | 1.29 | 0.2562 |
| bap*photoperiod | 4.4 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 8.8 | 8 | 1 | -0.4074 | 0.1686 | -0.7378 | -0.0769 | 5.84 | 0.0157 |
| bap*photoperiod | 8.8 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 17.6 | 8 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 17.6 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| Scale | 0 | 1.0000 | 0.0000 | 1.0000 | 1.0000 | ||||
| Note: | The scale parameter was held fixed. |
| Analysis Of Maximum Likelihood Zero Inflation Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | -0.1033 | 0.1766 | -0.4495 | 0.2429 | 0.34 | 0.5587 | |
| photoperiod | 8 | 1 | -4.1698 | 0.7611 | -5.6617 | -2.6780 | 30.01 | <.0001 |
| photoperiod | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
Another method for assessing the goodness-of-fit of the model is to compare the observed relative frequencies of the various counts to the maximum likelihood estimates of their respective probabilities. The following SAS statements demonstrate one method of computing the estimated probabilities and generating two comparative plots.
The first step is to observe the value of the largest count and the sample size and save them into macro variables.
proc means data=Trajan noprint; var roots; output out=maxcount max=max N=N; run;
data _null_;
set maxcount;
call symput('N',N);
call symput('max',max);
run;
%let max=%sysfunc(strip(&max));
Next, you use the model predictions and the estimated zero-inflation probabilities that are stored in the output data set Zip to compute the conditional probabilities ![]() . These are the variables
. These are the variables ep0–ep&max in the following DATA step. You also generate an indicator variable for each count ![]() ,
, ![]() , where each observation is assigned a value of 1 if count
, where each observation is assigned a value of 1 if count ![]() is observed, and 0 otherwise. These are the variables
is observed, and 0 otherwise. These are the variables c0–c&max.
data zip(drop= i);
set zip;
lambda=pred/(1-pzero);
array ep{0:&max} ep0-ep&max;
array c{0:&max} c0-c&max;
do i = 0 to &max;
if i=0 then ep{i}= pzero + (1-pzero)*pdf('POISSON',i,lambda);
else ep{i}= (1-pzero)*pdf('POISSON',i,lambda);
c{i}=ifn(roots=i,1,0);
end;
run;
Now you can use PROC MEANS to compute the means of the variables ep0, ![]() ,
, ep&max and c0, ![]() ,
, c&max. The means of ep0, ![]() ,
, ep&max are the maximum likelihood estimates of ![]() . The means of
. The means of c0, ![]() ,
, c&max are the observed relative frequencies.
proc means data=zip noprint; var ep0 - ep&max c0-c&max; output out=ep(drop=_TYPE_ _FREQ_) mean(ep0-ep&max)=ep0-ep&max; output out=p(drop=_TYPE_ _FREQ_) mean(c0-c&max)=p0-p&max; run;
The output data sets from PROC MEANS are in what is commonly referred to as wide form. That is, there is one observation for each variable. In order to generate comparative plots, the data need to be in what is referred to as long form. Ultimately, you need four variables, one whose observations are an index of the values of the counts, a second whose observations are the observed relative frequencies, a third whose observations contain the ZIP model estimates of the probabilities ![]() , and a fourth whose observations contain the difference between the observed relative frequencies and the estimated probabilities.
, and a fourth whose observations contain the difference between the observed relative frequencies and the estimated probabilities.
The following SAS statements transpose the two output data sets so that they are in long form. Then, the two data sets are merged and the variables that index the count values and record the difference between the observed relative frequencies and the estimated probabilities are generated.
proc transpose data=ep out=ep(rename=(col1=zip) drop=_NAME_); run; proc transpose data=p out=p(rename=(col1=p) drop=_NAME_); run;
data zipprob;
merge ep p;
zipdiff=p-zip;
roots=_N_ -1;
label zip='ZIP Probabilities'
p='Relative Frequencies'
zipdiff='Observed minus Predicted';
run;
Now you can use the SGPLOT procedure to produce the comparative plots.
proc sgplot data=zipprob;
scatter x=roots y=p /
markerattrs=(symbol=CircleFilled size=5px color=blue);
scatter x=roots y=zip /
markerattrs=(symbol=TriangleFilled size=5px color=red);
xaxis type=discrete;
run;
proc sgplot data=zipprob;
series x=roots y=zipdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=CircleFilled size=5px color=blue);
refline 0/ axis=y;
xaxis type=discrete;
run;
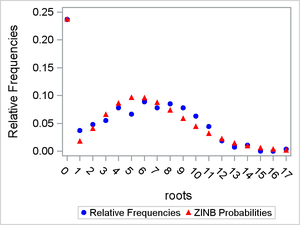
Figure 9: Comparison of ZIP Probabilities to Observed Relative Frequencies
Figure 9: Comparison of ZIP Probabilities to Observed Relative Frequencies
|
ZIP Probabilities versus Relative Frequencies |
Observed Relative Frequencies Minus ZIP Probabilities |
|
|
|
Figure 9 shows that the ZIP model accounts for the excess zeros quite well and that the ZIP distribution reasonably captures the shape of the distribution of the relative frequencies.
Clearly, a zero-inflated model can account for the excess zeros. However, because the Pearson statistic indicates that there is evidence of model misspecification, with overdispersion being the most likely culprit, inference based upon the ZIP model estimates are suspect. If overdispersion is the culprit, then fitting a zero-inflated negative binomial (ZINB) might be a solution because it can account for the excess zeros as well as the ZIP model did and it provides a more flexible estimator for the variance of the response variable.
The following SAS statements fit a ZINB model to the response variable Roots. The model specification is the same as before except that the DIST= option in the MODEL statement now specifies a ZINB distribution.
proc genmod data=Trajan; class bap photoperiod; model roots = bap|photoperiod / dist=zinb offset=lshoot; zeromodel photoperiod; output out=zinb predicted=pred pzero=pzero; ods output ParameterEstimates=zinbparms; ods output Modelfit=fit; run;
Output 4 displays the fit criteria for the ZINB model. The Pearson chi-square statistic divided by its degrees-of-freedom is 1.0313, which is much closer to 1 compared to the ZIP model.
Output 4: ZINB Model of Roots Data
| Criteria For Assessing Goodness Of Fit | |||
|---|---|---|---|
| Criterion | DF | Value | Value/DF |
| Deviance | 1232.4509 | ||
| Scaled Deviance | 1232.4509 | ||
| Pearson Chi-Square | 260 | 268.1486 | 1.0313 |
| Scaled Pearson X2 | 260 | 268.1486 | 1.0313 |
| Log Likelihood | -616.2255 | ||
| Full Log Likelihood | -616.2255 | ||
| AIC (smaller is better) | 1254.4509 | ||
| AICC (smaller is better) | 1255.4742 | ||
| BIC (smaller is better) | 1294.0336 | ||
The following SAS statements perform the same formal test that was used for the ZIP model:
data fit; set fit(where=(criterion="Scaled Pearson X2")); format pvalue pvalue6.4; pvalue=1-probchi(value,df); run;
proc print data=fit noobs; var criterion value df pvalue; run;
Output 5 reveals a p-value of 0.3509, which indicates that you would fail to reject the null hypothesis of no overdispersion at the most commonly used confidence levels.
Output 5: Pearson Chi-Square Statistic
| Criterion | Value | DF | pvalue |
|---|---|---|---|
| Scaled Pearson X2 | 268.1486 | 260 | 0.3509 |
Table 2 provides a side-by-side comparison of the other fit criteria for the two models. All of the criteria favor the ZINB over the ZIP model.
Table 2: Comparison of ZIP and ZINB Model Fit Criteria
|
Criterion |
ZIP |
ZINB |
|---|---|---|
|
Full Log Likelihood |
–622.2283 |
–616.2255 |
|
AIC |
1264.4566 |
1254.4509 |
|
AICC |
1265.3060 |
1255.4742 |
|
BIC |
1300.4408 |
1294.0336 |
Output 6 displays the ZINB model’s parameter estimates. Compared to the ZIP model, most (but not all) of the ZINB model parameters are slightly smaller in magnitude and the standard errors are larger. There is effectively no change in any inference you would make regarding any of the parameters. The negative binomial dispersion parameter has an estimated value of 0.0649, and the Wald 95% confidence interval indicates that the estimate is significantly different from 0.
Output 6: ZINB Model Parameter Estimates
The GENMOD Procedure
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |||
| Intercept | 1 | -2.1663 | 0.1188 | -2.3992 | -1.9333 | 332.22 | <.0001 | ||
| bap | 2.2 | 1 | 0.6371 | 0.1702 | 0.3036 | 0.9706 | 14.02 | 0.0002 | |
| bap | 4.4 | 1 | 0.5235 | 0.1777 | 0.1753 | 0.8717 | 8.68 | 0.0032 | |
| bap | 8.8 | 1 | 0.4095 | 0.1697 | 0.0769 | 0.7421 | 5.82 | 0.0158 | |
| bap | 17.6 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . | |
| photoperiod | 8 | 1 | 0.4875 | 0.1397 | 0.2137 | 0.7614 | 12.17 | 0.0005 | |
| photoperiod | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . | |
| bap*photoperiod | 2.2 | 8 | 1 | -0.5960 | 0.2055 | -0.9988 | -0.1931 | 8.41 | 0.0037 |
| bap*photoperiod | 2.2 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 4.4 | 8 | 1 | -0.1962 | 0.2084 | -0.6047 | 0.2123 | 0.89 | 0.3466 |
| bap*photoperiod | 4.4 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 8.8 | 8 | 1 | -0.4048 | 0.1979 | -0.7927 | -0.0169 | 4.18 | 0.0408 |
| bap*photoperiod | 8.8 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 17.6 | 8 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| bap*photoperiod | 17.6 | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
| Dispersion | 1 | 0.0649 | 0.0240 | 0.0314 | 0.1340 | ||||
| Note: | The negative binomial dispersion parameter was estimated by maximum likelihood. |
| Analysis Of Maximum Likelihood Zero Inflation Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | -0.1150 | 0.1779 | -0.4636 | 0.2336 | 0.42 | 0.5179 | |
| photoperiod | 8 | 1 | -4.2924 | 0.8694 | -5.9963 | -2.5885 | 24.38 | <.0001 |
| photoperiod | 16 | 0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | . | . |
You can generate comparative plots the same way as before with a few minor alterations. The values of the macro variables &max and &N have not changed, so you do not need to generate them a second time. You do need to capture the value of the negative binomial dispersion parameter in a macro variable, as demonstrated in the following DATA step:
data zinbparms;
set zinbparms(where=(Parameter="Dispersion"));
keep estimate;
call symput('k',estimate);
run;
You compute the maximum likelihood estimates of the marginal probabilities the same way as before except that you now specify a negative binomial distribution in the PDF function; this is where the macro variable &k that contains the negative binomial dispersion parameter is used.
data zinb(drop= i);
set zinb;
lambda=pred/(1-pzero);
k=&k;
array ep{0:&max} ep0-ep&max;
array c{0:&max} c0-c&max;
do i = 0 to &max;
if i=0 then ep{i}= pzero + (1-pzero)*pdf('NEGBINOMIAL',i,(1/(1+k*lambda)),(1/k));
else ep{i}= (1-pzero)*pdf('NEGBINOMIAL',i,(1/(1+k*lambda)),(1/k));
c{i}=ifn(roots=i,1,0);
end;
run;
The marginal probabilities are computed the same as before (by computing the means of the conditional probabilities) except that the input data set name for the MEANS procedure set has changed from ZIP to ZINB. The SAS statements that reshape the output data sets are the same as before except that the name of the data set that contains the results is now called Zinbprob, the variable that contains the estimated probabilities is called Zinb, and the variable that contains the difference between the observed relative frequencies and the estimated probabilities is named Zinbdiff.
proc means data=zinb noprint; var ep0 - ep&max c0-c&max; output out=ep(drop=_TYPE_ _FREQ_) mean(ep0-ep&max)=ep0-ep&max; output out=p(drop=_TYPE_ _FREQ_) mean(c0-c&max)=p0-p&max; run;
proc transpose data=ep out=ep(rename=(col1=zinb) drop=_NAME_); run; proc transpose data=p out=p(rename=(col1=p) drop=_NAME_); run;
data zinbprob;
merge ep p;
zinbdiff=p-zinb;
roots=_N_ -1;
label zinb='ZINB Probabilities'
p='Relative Frequencies'
zinbdiff='Observed minus Predicted';
run;
proc sgplot data=zinbprob;
scatter x=roots y=p /
markerattrs=(symbol=CircleFilled size=5px color=blue);
scatter x=roots y=zinb /
markerattrs=(symbol=TriangleFilled size=5px color=red);
xaxis type=discrete;
run;
proc sgplot data=zinbprob;
series x=roots y=zinbdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=CircleFilled size=5px color=blue);
refline 0/ axis=y;
xaxis type=discrete;
run;
Figure 10 displays the comparative plots for the ZINB model.
Figure 10: Comparison of ZINB Probabilities to Observed Relative Frequencies
|
ZINB Probabilities versus Relative Frequencies |
Observed Relative Frequencies Minus ZINB Probabilities |
|
|
|
You can also produce a plot that enables you to visually compare the fits of the ZIP and ZINB models. To do this, you merge the two data sets Zipprob and Zinbprob and plot the differences between the observed relative frequencies and the estimated marginal probabilities for both the ZIP and ZINB models.
The following DATA step merges the data sets Zipprob and Zinbprob, and then the SGPLOT procedure produces the comparative plot:
data compare; merge zipprob zinbprob; by roots; run;
proc sgplot data=compare;
series x=roots y=zinbdiff /
lineattrs=(pattern=Solid color=red)
markers markerattrs=(symbol=TriangleFilled color=red)
legendlabel="ZINB";
series x=roots y=zipdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=StarFilled color=blue)
legendlabel="ZIP";
refline 0/ axis=y;
xaxis type=discrete;
run;
Inspection of Figure 11 does not reveal any clear indication that one model fits better than the other.
Figure 11: Comparative Fit of ZIP and ZINB Models

The cumulative evidence suggests that the ZINB model provides an adequate fit to the data and that it is at least as good as, or superior to, the ZIP model for these data. With no evidence of overdispersion, it is reasonable to assume that the standard errors of the ZINB model’s parameter estimates are unbiased and that the model’s estimates are suitable for statistical inference.
It was clear from the graphical evidence at the outset that Photoperiod has a significant effect, and this is supported by the ZINB model results. The model also indicates that BAP is a significant predictor of the number of roots; but with both main and interaction effects, the relationship between the number of roots and the level of BAP is not readily apparent at first glance. An effect plot provides a useful graphical summary of the relationship between a model’s prediction and categorial predictor. For most models that you can fit with PROC GENMOD, you can request an effect plot by using the EFFECTPLOT statement. However, the EFFECTPLOT statement in PROC GENMOD in SAS/STAT 12.1 is not designed for use with zero-inflated models. Nevertheless, you can create an effect plot manually by using the following SAS statements:
proc sort data=zinb out=zinb; by photoperiod bap; run;
proc means data=zinb; var pred; by photoperiod bap; output out=effects mean(pred)=pred; run;
proc sgpanel data=effects;
panelby photoperiod;
series x=bap y=pred / markers
markerattrs=(symbol=CircleFilled size=5px color=red);
colaxis type=discrete;
run;
Figure 12 clearly shows that BAP has a negative, linear effect on the expected number of roots when Photoperiod = 16. However, the effect of BAP when Photoperiod = 8 is more complex; it appears to be nonlinear, first increasing, and then decreasing.
Figure 12: Effect of BAP by Photoperiod

References
-
Ridout, M. S., Hinde, J. P., and Demétrio, C. G. B. (1998), “Models for Count Data with Many Zeros,” in Proceedings of the 19th International Biometric Conference, 179–192, Cape Town.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
data Trajan;
input roots shoot photoperiod bap;
lshoot=log(shoot);
datalines;
0 40 8 17.6
0 40 8 17.6
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 2.2
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 4.4
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 30 16 8.8
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
0 40 16 17.6
1 30 8 2.2
1 30 8 2.2
1 30 8 2.2
1 30 16 4.4
1 30 16 4.4
1 30 16 8.8
1 30 16 8.8
1 30 16 8.8
1 40 16 17.6
1 40 16 17.6
2 30 8 2.2
2 30 8 2.2
2 30 8 4.4
2 30 8 4.4
2 30 8 4.4
2 40 8 8.8
2 30 16 2.2
2 30 16 2.2
2 30 16 4.4
2 30 16 8.8
2 30 16 8.8
2 40 16 17.6
2 40 16 17.6
3 30 8 2.2
3 30 8 2.2
3 30 8 2.2
3 40 8 8.8
3 40 8 8.8
3 40 8 17.6
3 40 8 17.6
3 30 16 2.2
3 30 16 2.2
3 30 16 4.4
3 30 16 8.8
3 40 16 17.6
3 40 16 17.6
3 40 16 17.6
3 40 16 17.6
4 30 8 2.2
4 30 8 2.2
4 30 8 2.2
4 30 8 2.2
4 30 8 2.2
4 30 8 2.2
4 30 8 4.4
4 40 8 8.8
4 40 8 8.8
4 40 8 8.8
4 40 8 8.8
4 40 8 17.6
4 40 8 17.6
4 30 16 2.2
4 30 16 4.4
4 30 16 4.4
4 30 16 8.8
4 30 16 8.8
4 40 16 17.6
4 40 16 17.6
4 40 16 17.6
5 30 8 2.2
5 30 8 2.2
5 30 8 2.2
5 40 8 8.8
5 40 8 8.8
5 40 8 8.8
5 40 8 8.8
5 40 8 17.6
5 40 8 17.6
5 40 8 17.6
5 40 8 17.6
5 40 8 17.6
5 30 16 2.2
5 30 16 2.2
5 30 16 4.4
5 30 16 8.8
5 30 16 8.8
5 40 16 17.6
6 30 8 2.2
6 30 8 2.2
6 30 8 4.4
6 30 8 4.4
6 30 8 4.4
6 40 8 8.8
6 40 8 8.8
6 40 8 8.8
6 40 8 8.8
6 40 8 17.6
6 40 8 17.6
6 40 8 17.6
6 40 8 17.6
6 40 8 17.6
6 30 16 2.2
6 30 16 4.4
6 30 16 4.4
6 30 16 8.8
6 30 16 8.8
6 30 16 8.8
6 40 16 17.6
6 40 16 17.6
6 40 16 17.6
6 40 16 17.6
7 30 8 2.2
7 30 8 2.2
7 30 8 4.4
7 30 8 4.4
7 30 8 4.4
7 30 8 4.4
7 30 8 4.4
7 30 8 4.4
7 30 8 4.4
7 40 8 8.8
7 40 8 8.8
7 40 8 8.8
7 40 8 8.8
7 40 8 17.6
7 40 8 17.6
7 40 8 17.6
7 40 8 17.6
7 30 16 8.8
7 40 16 17.6
7 40 16 17.6
7 40 16 17.6
8 30 8 2.2
8 30 8 2.2
8 30 8 2.2
8 30 8 4.4
8 30 8 4.4
8 30 8 4.4
8 40 8 8.8
8 40 8 8.8
8 40 8 8.8
8 40 8 8.8
8 40 8 8.8
8 40 8 8.8
8 40 8 8.8
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 40 8 17.6
8 30 16 2.2
8 30 16 4.4
9 30 8 2.2
9 30 8 4.4
9 30 8 4.4
9 30 8 4.4
9 30 8 4.4
9 30 8 4.4
9 40 8 8.8
9 40 8 8.8
9 40 8 8.8
9 40 8 8.8
9 40 8 8.8
9 40 8 17.6
9 40 8 17.6
9 40 8 17.6
9 30 16 2.2
9 30 16 2.2
9 30 16 2.2
9 30 16 8.8
9 30 16 8.8
9 40 16 17.6
9 40 16 17.6
10 30 8 2.2
10 30 8 2.2
10 30 8 4.4
10 30 8 4.4
10 30 8 4.4
10 40 8 8.8
10 40 8 8.8
10 40 8 8.8
10 40 8 8.8
10 40 8 17.6
10 40 8 17.6
10 40 8 17.6
10 40 8 17.6
10 30 16 2.2
10 30 16 4.4
10 30 16 4.4
10 30 16 4.4
11 30 8 2.2
11 30 8 4.4
11 30 8 4.4
11 30 8 4.4
11 30 8 4.4
11 40 8 8.8
11 40 8 17.6
11 40 8 17.6
11 40 8 17.6
11 40 8 17.6
11 30 16 2.2
11 30 16 8.8
12 40 8 8.8
12 40 8 8.8
12 30 16 2.2
12 30 16 4.4
12 30 16 8.8
13 30 8 2.2
13 30 8 4.4
14 40 8 8.8
14 40 8 8.8
14 40 8 17.6
17 30 8 2.2
;
ods graphics on;
proc freq data=Trajan;
table roots / plots(only)=freqplot(scale=percent);
run;
proc sort data=Trajan out=Trajan;
by photoperiod;
run;
proc freq data=Trajan;
table roots / plots(only)=freqplot(scale=percent);
by photoperiod;
run;
proc sort data=Trajan out=Trajan;
by bap;
run;
proc freq data=Trajan;
table roots / plots(only)=freqplot(scale=percent);
by bap;
run;
proc sort data=Trajan out=Trajan;
by photoperiod bap;
run;
proc freq data=Trajan;
table roots / plots(only)=freqplot(scale=percent);
by photoperiod bap;
run;
proc genmod data=Trajan;
class bap photoperiod;
model roots = bap|photoperiod / dist=zip offset=lshoot;
zeromodel photoperiod;
output out=zip predicted=pred pzero=pzero;
ods output Modelfit=fit;
run;
data fit;
set fit(where=(criterion="Scaled Pearson X2"));
format pvalue pvalue6.4;
pvalue=1-probchi(value,df);
run;
proc print data=fit noobs;
var criterion value df pvalue;
run;
proc means data=Trajan noprint;
var roots;
output out=maxcount max=max N=N;
run;
data _null_;
set maxcount;
call symput('N',N);
call symput('max',max);
run;
%let max=%sysfunc(strip(&max));
data zip(drop= i);
set zip;
lambda=pred/(1-pzero);
array ep{0:&max} ep0-ep&max;
array c{0:&max} c0-c&max;
do i = 0 to &max;
if i=0 then ep{i}= pzero + (1-pzero)*pdf('POISSON',i,lambda);
else ep{i}= (1-pzero)*pdf('POISSON',i,lambda);
c{i}=ifn(roots=i,1,0);
end;
run;
proc means data=zip noprint;
var ep0 - ep&max c0-c&max;
output out=ep(drop=_TYPE_ _FREQ_) mean(ep0-ep&max)=ep0-ep&max;
output out=p(drop=_TYPE_ _FREQ_) mean(c0-c&max)=p0-p&max;
run;
proc transpose data=ep out=ep(rename=(col1=zip) drop=_NAME_);
run;
proc transpose data=p out=p(rename=(col1=p) drop=_NAME_);
run;
data zipprob;
merge ep p;
zipdiff=p-zip;
roots=_N_ -1;
label zip='ZIP Probabilities'
p='Relative Frequencies'
zipdiff='Observed minus Predicted';
run;
proc sgplot data=zipprob;
scatter x=roots y=p /
markerattrs=(symbol=CircleFilled size=5px color=blue);
scatter x=roots y=zip /
markerattrs=(symbol=TriangleFilled size=5px color=red);
xaxis type=discrete;
run;
proc sgplot data=zipprob;
series x=roots y=zipdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=CircleFilled size=5px color=blue);
refline 0/ axis=y;
xaxis type=discrete;
run;
proc genmod data=Trajan;
class bap photoperiod;
model roots = bap|photoperiod / dist=zinb offset=lshoot;
zeromodel photoperiod;
output out=zinb predicted=pred pzero=pzero;
ods output ParameterEstimates=zinbparms;
ods output Modelfit=fit;
run;
data fit;
set fit(where=(criterion="Scaled Pearson X2"));
format pvalue pvalue6.4;
pvalue=1-probchi(value,df);
run;
proc print data=fit noobs;
var criterion value df pvalue;
run;
data zinbparms;
set zinbparms(where=(Parameter="Dispersion"));
keep estimate;
call symput('k',estimate);
run;
data zinb(drop= i);
set zinb;
lambda=pred/(1-pzero);
k=&k;
array ep{0:&max} ep0-ep&max;
array c{0:&max} c0-c&max;
do i = 0 to &max;
if i=0 then ep{i}= pzero + (1-pzero)*pdf('NEGBINOMIAL',i,(1/(1+k*lambda)),(1/k));
else ep{i}= (1-pzero)*pdf('NEGBINOMIAL',i,(1/(1+k*lambda)),(1/k));
c{i}=ifn(roots=i,1,0);
end;
run;
proc means data=zinb noprint;
var ep0 - ep&max c0-c&max;
output out=ep(drop=_TYPE_ _FREQ_) mean(ep0-ep&max)=ep0-ep&max;
output out=p(drop=_TYPE_ _FREQ_) mean(c0-c&max)=p0-p&max;
run;
proc transpose data=ep out=ep(rename=(col1=zinb) drop=_NAME_);
run;
proc transpose data=p out=p(rename=(col1=p) drop=_NAME_);
run;
data zinbprob;
merge ep p;
zinbdiff=p-zinb;
roots=_N_ -1;
label zinb='ZINB Probabilities'
p='Relative Frequencies'
zinbdiff='Observed minus Predicted';
run;
proc sgplot data=zinbprob;
scatter x=roots y=p /
markerattrs=(symbol=CircleFilled size=5px color=blue);
scatter x=roots y=zinb /
markerattrs=(symbol=TriangleFilled size=5px color=red);
xaxis type=discrete;
run;
proc sgplot data=zinbprob;
series x=roots y=zinbdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=CircleFilled size=5px color=blue);
refline 0/ axis=y;
xaxis type=discrete;
run;
data compare;
merge zipprob zinbprob;
by roots;
run;
proc sgplot data=compare;
series x=roots y=zinbdiff /
lineattrs=(pattern=Solid color=red)
markers markerattrs=(symbol=TriangleFilled color=red)
legendlabel="ZINB";
series x=roots y=zipdiff /
lineattrs=(pattern=ShortDash color=blue)
markers markerattrs=(symbol=StarFilled color=blue)
legendlabel="ZIP";
refline 0/ axis=y;
xaxis type=discrete;
run;
proc sort data=zinb out=zinb;
by photoperiod bap;
run;
proc means data=zinb;
var pred;
by photoperiod bap;
output out=effects mean(pred)=pred;
run;
proc sgpanel data=effects;
panelby photoperiod;
series x=bap y=pred / markers
markerattrs=(symbol=CircleFilled size=5px color=red);
colaxis type=discrete;
run;
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
| Type: | Sample |
| Topic: | SAS Reference ==> Procedures ==> GENMOD |
| Date Modified: | 2017-01-12 16:10:16 |
| Date Created: | 2016-10-25 16:01:37 |
Operating System and Release Information
| Product Family | Product | Host | SAS Release | |
| Starting | Ending | |||
| SAS System | SAS/STAT | z/OS | ||
| z/OS 64-bit | ||||
| OpenVMS VAX | ||||
| Microsoft® Windows® for 64-Bit Itanium-based Systems | ||||
| Microsoft Windows Server 2003 Datacenter 64-bit Edition | ||||
| Microsoft Windows Server 2003 Enterprise 64-bit Edition | ||||
| Microsoft Windows XP 64-bit Edition | ||||
| Microsoft® Windows® for x64 | ||||
| OS/2 | ||||
| Microsoft Windows 8 Enterprise 32-bit | ||||
| Microsoft Windows 8 Enterprise x64 | ||||
| Microsoft Windows 8 Pro 32-bit | ||||
| Microsoft Windows 8 Pro x64 | ||||
| Microsoft Windows 8.1 Enterprise 32-bit | ||||
| Microsoft Windows 8.1 Enterprise x64 | ||||
| Microsoft Windows 8.1 Pro 32-bit | ||||
| Microsoft Windows 8.1 Pro x64 | ||||
| Microsoft Windows 10 | ||||
| Microsoft Windows 95/98 | ||||
| Microsoft Windows 2000 Advanced Server | ||||
| Microsoft Windows 2000 Datacenter Server | ||||
| Microsoft Windows 2000 Server | ||||
| Microsoft Windows 2000 Professional | ||||
| Microsoft Windows NT Workstation | ||||
| Microsoft Windows Server 2003 Datacenter Edition | ||||
| Microsoft Windows Server 2003 Enterprise Edition | ||||
| Microsoft Windows Server 2003 Standard Edition | ||||
| Microsoft Windows Server 2003 for x64 | ||||
| Microsoft Windows Server 2008 | ||||
| Microsoft Windows Server 2008 R2 | ||||
| Microsoft Windows Server 2008 for x64 | ||||
| Microsoft Windows Server 2012 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Datacenter | ||||
| Microsoft Windows Server 2012 R2 Std | ||||
| Microsoft Windows Server 2012 Std | ||||
| Microsoft Windows XP Professional | ||||
| Windows 7 Enterprise 32 bit | ||||
| Windows 7 Enterprise x64 | ||||
| Windows 7 Home Premium 32 bit | ||||
| Windows 7 Home Premium x64 | ||||
| Windows 7 Professional 32 bit | ||||
| Windows 7 Professional x64 | ||||
| Windows 7 Ultimate 32 bit | ||||
| Windows 7 Ultimate x64 | ||||
| Windows Millennium Edition (Me) | ||||
| Windows Vista | ||||
| Windows Vista for x64 | ||||
| 64-bit Enabled AIX | ||||
| 64-bit Enabled HP-UX | ||||
| 64-bit Enabled Solaris | ||||
| ABI+ for Intel Architecture | ||||
| AIX | ||||
| HP-UX | ||||
| HP-UX IPF | ||||
| IRIX | ||||
| Linux | ||||
| Linux for x64 | ||||
| Linux on Itanium | ||||
| OpenVMS Alpha | ||||
| OpenVMS on HP Integrity | ||||
| Solaris | ||||
| Solaris for x64 | ||||
| Tru64 UNIX | ||||