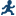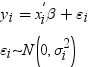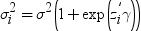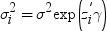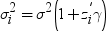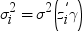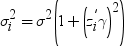Binary Probit/Logit Regression Task

About the Binary Probit/Logit Regression Task

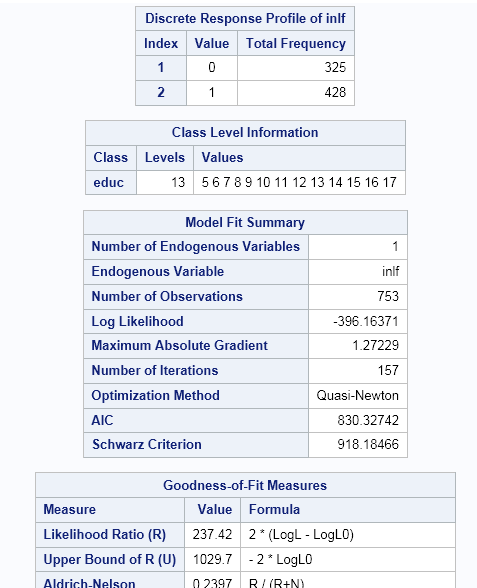
The Binary Probit/Logit Regression task analyzes univariate dependent variable models. In these models, the dependent variable takes binary values and assumes either a standard normal distribution or a logistic distribution.
Note: The version of the task depends on what version of SAS/ETS is available at your site. For example, if your site is running the second maintenance release for SAS 9.3, SAS/ETS 12.1 is available, and SAS Studio is running version 1 of the Binary Probit/Logit Regression task. If you are running SAS 9.4, SAS/ETS 12.3 is available, and SAS Studio is running version 2 of the Binary Probit/Logit Regression task. The difference between the two versions is the addition of new options in SAS/ETS 12.3.

Example: Binary Probit/Logit Regression Task

To create this example:
  1. Create the Work.Mroz data set. For more information, see MROZ Data Set.
  2. In the Tasks section, expand the Econometrics folder and double-click Probit/Logit Regression. The user interface for the Probit/Logit Regression task opens.
  3. On the Data tab, select the WORK.MROZ data set.
  4. Assign columns to these roles:
    Role
    Column Name
    Dependent variable
    inlf
    Continuous variables
    nwifeinc
    exper
    expersq
    age
    kidslt6
    kidsge6
    Categorical variables
    educ
  5. To run the task, click Submit SAS code.
Here is a subset of the results:
Example of the Results from Probit/Logit Task

Assigning Data to Roles

To run the Binary Probit/Logit Regression task, you must assign a column to the Dependent variable role.
Role
Description
Dependent variable
specifies the numeric column to use as the dependent variable for the regression analysis.
Use the Distribution drop-down list to specify whether to create a normal or logistic model.
Continuous variables
specifies the numeric columns to use as the independent regressor (explanatory) variables for the regression model.
Categorical variables
specifies how to group values into levels.

Setting Options

Option
Description
Methods
Type of covariances of the parameter estimates
specifies the type of covariance matrix of the parameter estimates.
You can specify these types of matrices:
  • the covariance from the inverse Hessian matrix
  • the covariance from the outer product mix
  • the covariance from the outer product and Hessian matrices (also called the quasi-maximum-likelihood-estimates)
Include the intercept in the model
specifies whether to include the intercept in the model.
Optimization
Method
specifies the iterative minimization method to use. By default, the Quasi-Newton method is used.
Maximum number of iterations
specifies the maximum number of iterations for the selected method.
Heteroscedasticity
Variables on the variance function
specifies the columns that are related to heteroscedasticity of the residuals and how these variables are used to model error variances. Here is the heteroscedastic regression model that is supported by this task: y sub i , equals , x with subscript i , and with superscript prime , end sub-superscript , beta plus , epsilon sub i end sub , epsilon sub i , tilde n open 0 comma , sigma sub i and super 2 , close
Form of variance function
specifies the link function to use. You can choose from these options:
  • Exponential sigma sub i and super 2 , equals , sigma squared , open 1 plus exp of open , z with subscript i , and with superscript prime , end sub-superscript , gamma close close
  • Exponential with no constant sigma sub i and super 2 , equals , sigma squared , exp of open , z with subscript i , and with superscript prime , end sub-superscript , gamma close
  • Linear sigma sub i and super 2 , equals , sigma squared , open 1 plus , z with subscript i , and with superscript prime , end sub-superscript , gamma close
  • Linear with no constant sigma sub i and super 2 , equals , sigma squared , open , z with subscript i , and with superscript prime , end sub-superscript , gamma close
  • Square of linear function sigma sub i and super 2 , equals , sigma squared , open 1 plus . open , z with subscript i , and with superscript prime , end sub-superscript , gamma close squared . close
  • Square of linear function with no constant sigma sub i and super 2 , equals , sigma squared . open , z with subscript i , and with superscript prime , end sub-superscript , gamma close squared

Setting Output Options

Option
Description
Plots
Diagnostic Plots
Error standard deviations by observed regressor
displays the error standard deviation versus observed regressors when you assign a column to the Variables on the variance function option.
Profiled log likelihood
displays the profiled log likelihood. Each profiled graph is obtained by setting all the parameters to their maximum likelihood estimate except for the profiling parameter. The profiling parameter takes values on a predefined grid that is determined by the maximum likelihood estimate of the corresponding standard deviation.
Output Plots
Predicted values by regressor
displays the model predicted values. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Marginal effects by regressor
displays the marginal effects. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Inverse Mills ratio by regressor
displays the inverse Mills ratio. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Predicted response probability by regressor
displays the predicted response probability. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Predicted probabilities for each level of the response by regressor
displays the predicted probabilities for each level of the response. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Linear predictor values by regressor
displays the structural part on the right side of the model. Each contributing regressor is set equal to its mean, except for the parameter that is reported on the X axis.
Display plots
specifies whether to display the plots in a panel or individually.
Output Tables
You can specify whether to include any output tables in the results.
Here is the information that you can include in the results:
  • correlation matrix of the parameter estimates
  • covariance matrix of the parameter estimates
  • iteration history of the objective function and parameter estimates
Copyright © SAS Institute Inc. All rights reserved.