The SURVEYSELECT Procedure
Proportional Allocation
When you specify the ALLOC=PROPORTIONAL option in the STRATA statement, PROC SURVEYSELECT allocates the total sample size among the strata in proportion to the stratum sizes, where the stratum size is the number of sampling units in the stratum. The allocation proportion of the total sample size for stratum h is
![\[ f_ h^{*} = N_ h / N \]](images/statug_surveyselect0109.png)
where 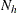 is the number of sampling units in stratum h and N is the total number of sampling units for all strata. If you specify the total sample size n in the SAMPSIZE=
option in the PROC SURVEYSELECT
statement, the procedure computes the target sample size for stratum h as
is the number of sampling units in stratum h and N is the total number of sampling units for all strata. If you specify the total sample size n in the SAMPSIZE=
option in the PROC SURVEYSELECT
statement, the procedure computes the target sample size for stratum h as
![\[ n_ h^{*} = f_ h^{*} \times n \]](images/statug_surveyselect0110.png)
The target sample size values, 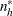 , might not be integers, but the stratum sample sizes are required to be integers. PROC SURVEYSELECT uses a rounding algorithm
to convert the
, might not be integers, but the stratum sample sizes are required to be integers. PROC SURVEYSELECT uses a rounding algorithm
to convert the 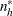 to integer values
to integer values 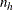 and maintain the requested total sample size n. The rounding algorithm includes the restriction that all values of
and maintain the requested total sample size n. The rounding algorithm includes the restriction that all values of 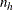 must be at least 1, so that at least one unit is selected from each stratum. If you specify a minimum stratum sample size
must be at least 1, so that at least one unit is selected from each stratum. If you specify a minimum stratum sample size
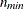 in the ALLOCMIN=
option in the STRATA
statement, then all values of
in the ALLOCMIN=
option in the STRATA
statement, then all values of 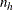 are required to be at least
are required to be at least 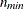 . For without-replacement selection methods, PROC SURVEYSELECT also requires that each stratum sample size must not exceed
the total number of sampling units in the stratum,
. For without-replacement selection methods, PROC SURVEYSELECT also requires that each stratum sample size must not exceed
the total number of sampling units in the stratum, 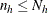 . If a target stratum sample size exceeds the number of units in the stratum, PROC SURVEYSELECT allocates the maximum number
of units,
. If a target stratum sample size exceeds the number of units in the stratum, PROC SURVEYSELECT allocates the maximum number
of units, 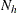 , to the stratum, and then allocates the remaining total sample size proportionally among the remaining strata.
, to the stratum, and then allocates the remaining total sample size proportionally among the remaining strata.
PROC SURVEYSELECT provides the target allocation proportions 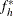 in the output data set variable
in the output data set variable AllocProportion. The variable ActualProportion contains the actual proportions for the allocated sample sizes 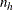 . For stratum h, the actual proportion is computed as
. For stratum h, the actual proportion is computed as
![\[ f_ h = n_ h / n \]](images/statug_surveyselect0115.png)
where 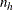 is the allocated sample size for stratum h and n is the total sample size. The actual proportions
is the allocated sample size for stratum h and n is the total sample size. The actual proportions 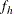 can differ from the target allocation proportions
can differ from the target allocation proportions 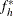 because of rounding, the requirement that
because of rounding, the requirement that 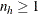 (or
(or 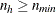 ), and the requirement that
), and the requirement that 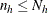 for without-replacement selection methods.
for without-replacement selection methods.
