The SURVEYSELECT Procedure

Brewer’s PPS Method

Brewer’s method (METHOD=PPS_BREWER ) selects two units from each stratum, with probability proportional to size and without replacement. The selection probability for unit i in stratum h is 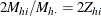$2M_{hi}/M_{h \cdot } = 2 Z_{hi}$ . (Because selection probabilities cannot exceed 1, the relative size for each unit, 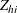$Z_{hi}$ , must not exceed $1/2$ .)

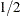Brewer’s algorithm first selects a unit with probability

$\frac{Z_{hi} (1-Z_{hi})}{D_ h (1-2Z_{hi})}$

where

$D_ h = \sum _{i=1}^{N_ h} \frac{Z_{hi} (1-Z_{hi})}{1-2Z_{hi}}$

Then a second unit is selected from the remaining units with probability

$\frac{Z_{hj}}{1-Z_{hi}}$

where unit i is the first unit selected. The joint selection probability for units i and j in stratum h is

$P_{h(ij)} = \frac{2 Z_{hi} Z_{hj}}{D_ h} \left( \frac{1 - Z_{hi} - Z_{hj}}{(1-2Z_{hi}) (1-2Z_{hj})} \right)$

For more information, see Cochran (1977, pp. 261–263) and Brewer (1963). Brewer’s method yields the same selection probabilities and joint selection probabilities as Durbin’s method (Cochran 1977; Durbin 1967).