The SURVEYFREQ Procedure

The Jackknife Method

If you specify the VARMETHOD=JACKKNIFE option, PROC SURVEYFREQ uses the delete-1 jackknife method for variance estimation. The jackknife method can be used for stratified sample designs and for designs with no stratification. If your design is stratified, the jackknife method requires at least two PSUs in each stratum. You can provide replicate weights for jackknife variance estimation by using a REPWEIGHTS statement, or the procedure can construct replicate weights for the analysis. PROC SURVEYFREQ estimates the parameter of interest (a proportion, total, odds ratio, or other statistic) from each replicate, and then uses the variability among replicate estimates to estimate the overall variance of the parameter estimate. For more information about jackknife variance estimation, see Wolter (1985) and Lohr (2010).

If you do not provide replicate weights with a REPWEIGHTS statement, PROC SURVEYFREQ constructs the replicates. The number of replicates R is the number of PSUs, and the procedure deletes one PSU from the full sample to form each replicate. The sampling weights are modified by the jackknife coefficient for the replicate to create the replicate weights.

If your design is not stratified (no STRATA statement), the jackknife coefficient has the same value for each replicate r. The jackknife coefficient is

\[ \alpha _ r = (R-1) / R \hspace{.15in} \mr{for} \hspace{.05in} r=1,2,\ldots ,R \]

where R is the total number of replicates (or total number of PSUs). For the PSUs included in a replicate, the replicate weights are computed by dividing the original sampling weights by the jackknife coefficient. For the deleted PSU, which is not included in the replicate, the replicate weights equal 0. The replicate weight for the jth member of the ith PSU can be expressed as follows when the design is not stratified:

\[ W^{r}_{ij} = \left\{ \begin{array}{lll} W_{ij} / \alpha _ r \hspace{.1in} & \mbox{if PSU } i \mbox{ is included in replicate } r \\[0.10in] 0 & \mr{otherwise} \\ \end{array} \right. \]

where $W_{ij}$ is the original sampling weight of unit $(ij)$, r is the replicate number, and $\alpha _ r$ is the jackknife coefficient.

If your design is stratified, the jackknife method requires at least two PSUs in each stratum. Let stratum $h_ r^{~ \prime }$ be the stratum from which a PSU is deleted to form the rth replicate. Stratum $h_ r^{~ \prime }$ is called the donor stratum. The jackknife coefficients are defined as

\[ \alpha _ r = (n_{h_ r^{~ \prime }} - 1 ) / n_{h_ r^{~ \prime }} \hspace{.15in} \mr{for} \hspace{.05in} r=1,2, \ldots , R \]

where $n_{h_ r^{~ \prime }}$ is the total number of PSUs in the donor stratum for replicate r. For all strata other than the donor stratum, the replicate r weights equal the original sampling weights. For PSUs included from the donor stratum, the replicate weights are computed by dividing the original sampling weights by the jackknife coefficient. For the deleted PSU, which is not included in the replicate, the replicate weights equal 0. The replicate weight for the jth member of the ith PSU in stratum h can be expressed as

\[ W^{r}_{hij} = \left\{ \begin{array}{lll} W_{hij} & \mr{if} \hspace{.05in} h \neq h_ r^{~ \prime } \\[0.10in] W_{hij} / \alpha _ r & \mr{if} \hspace{.05in} h = h_ r^{~ \prime } \hspace{.1in} \mbox{and PSU } (hi) \mbox{ is included in replicate } r \\[0.10in] 0 & \mr{if} \hspace{.05in} h = h_ r^{~ \prime } \hspace{.1in} \mbox{and PSU } (hi) \mbox{ is not included in replicate } r \end{array} \right. \]

You can use the OUTWEIGHTS= method-option to store the replicate weights in a SAS data set. You can also use the OUTJKCOEFS= method-option to store the jackknife coefficients in a SAS data set. For information about the contents of these output data sets, see the sections Jackknife Coefficient Output Data Set and Replicate Weight Output Data Set. You can provide replicate weights and jackknife coefficients to the procedure for subsequent analyses by using a REPWEIGHTS statement. If you provide replicate weights but do not provide jackknife coefficients, PROC SURVEYFREQ uses $\alpha _ r = (R-1)/ R$ as the jackknife coefficient for all replicates.

Let 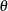$\theta $ denote the population parameter to be estimated—for example, a proportion, total, odds ratio, or other statistic. Let 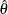$\hat{\theta }$ denote the estimate of 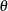$\theta $ from the full sample, and let 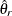$\hat{\theta }_ r$ be the estimate from the rth jackknife replicate, which is computed by using the replicate weights. The jackknife variance estimate for 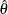$\hat{\theta }$ is computed as

\[ \widehat{V}(\hat{\theta }) = \sum _{r=1}^ R \alpha _ r \left( \hat{\theta }_ r - \hat{\theta } \right)^2 \]

where R is the total number of replicates and $\alpha _ r$ is the jackknife coefficient for replicate r.

If a parameter cannot be estimated from some replicate(s), then the variance estimate is computed by using those replicates from which the parameter can be estimated. For example, suppose the parameter is a column proportion—the proportion of column j for table cell (i, j). If a replicate r contains no observations in column j, then the column j proportion is not estimable from replicate r. In this case, the jackknife variance estimate is computed as

\[ \widehat{V}(\hat{\theta }) = \frac{R}{R'} \sum _{r=1}^{R'} \alpha _ r \left( \hat{\theta }_ r - \hat{\theta } \right)^2 \]

where the summation is over the replicates where the parameter 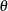$\theta $ is estimable, and 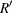$R’$ is the number of those replicates.