Introduction to Survey Sampling and Analysis Procedures

If you use Taylor series variance estimation, the survey procedures include a finite population correction factor in the analysis if you input either the sampling rate or the population total.

The sampling rate is the ratio of the sample size (the number of sampling units in the sample) n to the population size (the total number of sampling units in the target population) N, 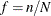. This ratio is also called the sampling fraction. If you select a sample without replacement, the extra efficiency compared to selecting a sample with replacement can be measured by the finite population correction (fpc) factor, (1-f).

To include a finite population correction factor in your analysis, you can input either the sampling rate or the population total. Otherwise, the procedures do not use the fpc in computing variance estimates. For fairly small sampling fractions, it is appropriate to ignore this correction. For more information, see Cochran (1977) and Kish (1965).

As discussed in the section Variance Estimation, for a multistage sample design, the procedures use only the first stage of the sample design for variance estimation. Therefore, if you are specifying the sampling rate, you should input the first-stage sampling rate, which is the ratio of the number of PSUs in the sample to the total number of PSUs in the target population.

If you use BRR or jackknife variance estimate, the procedures do not include a finite population correction in the analysis, and you do not need to input the sampling rate or the population total.