Introduction to Regression Procedures

Allen, D. M. (1971). “Mean Square Error of Prediction as a Criterion for Selecting Variables.” Technometrics 13:469–475.

Allen, D. M., and Cady, F. B. (1982). Analyzing Experimental Data by Regression. Belmont, CA: Lifetime Learning Publications.

Belsley, D. A., Kuh, E., and Welsch, R. E. (1980). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. New York: John Wiley & Sons.

Bock, R. D. (1975). Multivariate Statistical Methods in Behavioral Research. New York: McGraw-Hill.

Box, G. E. P. (1966). “The Use and Abuse of Regression.” Technometrics 8:625–629.

Box, G. E. P., and Cox, D. R. (1964). “An Analysis of Transformations.” Journal of the Royal Statistical Society, Series B 26:211–234.

Cleveland, W. S., Devlin, S. J., and Grosse, E. (1988). “Regression by Local Fitting.” Journal of Econometrics 37:87–114.

Cook, R. D. (1977). “Detection of Influential Observations in Linear Regression.” Technometrics 19:15–18.

Cook, R. D. (1979). “Influential Observations in Linear Regression.” Journal of the American Statistical Association 74:169–174.

Daniel, C., and Wood, F. S. (1999). Fitting Equations to Data: Computer Analysis of Multifactor Data. 2nd ed. New York: John Wiley & Sons.

Darlington, R. B. (1968). “Multiple Regression in Psychological Research and Practice.” Psychological Bulletin 69:161–182.

Davis, A. W. (1970). “Differential Equation of Hotelling’s Generalized .” Annals of Statistics 39:815–832.

Davis, A. W. (1972). “On the Marginal Distributions of the Latent Roots of the Multivariate Beta Matrix.” Biometrika 43:1664–1670.

Davis, A. W. (1979). “On the Differential Equation for Meijer’s Function, and Further Tables of Wilks’s Likelihood Ratio Criterion.” Biometrika 66:519–531.

Davis, A. W. (1980). “Further Tabulation of Hotelling’s Generalized .” Communications in Statistics—Simulation and Computation 9:321–336.

Draper, N. R., and Smith, H. (1998). Applied Regression Analysis. 3rd ed. New York: John Wiley & Sons.

Durbin, J., and Watson, G. S. (1951). “Testing for Serial Correlation in Least Squares Regression.” Biometrika 37:409–428.

Efron, B., Hastie, T. J., Johnstone, I. M., and Tibshirani, R. (2004). “Least Angle Regression (with Discussion).” Annals of Statistics 32:407–499.

Eilers, P. H. C., and Marx, B. D. (1996). “Flexible Smoothing with B-Splines and Penalties.” Statistical Science 11:89–121. With discussion.

Freund, R. J., and Littell, R. C. (1986). SAS System for Regression. 1986 ed. Cary, NC: SAS Institute Inc.

Freund, R. J., Littell, R. C., and Spector, P. C. (1991). SAS System for Linear Models. Cary, NC: SAS Institute Inc.

Friedman, J. H. (1991). “Multivariate Adaptive Regression Splines.” Annals of Statistics 19:1–67.

Gentleman, W. M. (1972). Basic Procedures for Large, Sparse, or Weighted Least Squares Problems. Technical Report CSRR-2068, University of Waterloo, Ontario.

Gentleman, W. M. (1973). “Least Squares Computations by Givens Transformations without Square Roots.” Journal of the Institute of Mathematics and Its Applications 12:329–336.

Goodnight, J. H. (1979). “A Tutorial on the Sweep Operator.” American Statistician 33:149–158.

Hawkins, D. M. (1980). “A Note on Fitting a Regression with No Intercept Term.” American Statistician 34:233.

Hosmer, D. W., Jr., and Lemeshow, S. (1989). Applied Logistic Regression. New York: John Wiley & Sons.

Huber, P. J. (1973). “Robust Regression: Asymptotics, Conjectures, and Monte Carlo.” Annals of Statistics 1:799–821.

Johnston, J., and DiNardo, J. (1997). Econometric Methods. 4th ed. New York: McGraw-Hill.

Kennedy, W. J., Jr., and Gentle, J. E. (1980). Statistical Computing. New York: Marcel Dekker.

Kvalseth, T. O. (1985). “Cautionary Note about .” American Statistician 39:279–285.

Lee, Y. (1972). “Some Results on the Distribution of Wilks’ Likelihood Ratio Criterion.” Biometrika 95:649.

Mallows, C. L. (1973). “Some Comments on 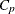.” Technometrics 15:661–675.

Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979). Multivariate Analysis. London: Academic Press.

Morrison, D. F. (2004). Multivariate Statistical Methods. 4th ed. New York: Duxbury Press.

Mosteller, F., and Tukey, J. W. (1977). Data Analysis and Regression. Reading, MA: Addison-Wesley.

Muller, K. E. (1998). “A New F Approximation for the Pillai-Bartlett Trace under .” Journal of Computational and Graphical Statistics 7:131–137.

Neter, J., and Wasserman, W. (1974). Applied Linear Statistical Models. Homewood, IL: Irwin.

Pillai, K. C. S. (1960). Statistical Table for Tests of Multivariate Hypotheses. Manila: University of Philippines Statistical Center.

Pillai, K. C. S., and Flury, B. N. (1984). “Percentage Points of the Largest Characteristic Root of the Multivariate Beta Matrix.” Communications in Statistics—Theory and Methods 13:2199–2237.

Pindyck, R. S., and Rubinfeld, D. L. (1981). Econometric Models and Econometric Forecasts. 2nd ed. New York: McGraw-Hill.

Rao, C. R. (1973). Linear Statistical Inference and Its Applications. 2nd ed. New York: John Wiley & Sons.

Rawlings, J. O. (1988). Applied Regression Analysis: A Research Tool. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software.

Rousseeuw, P. J. (1984). “Least Median of Squares Regression.” Journal of the American Statistical Association 79:871–880.

Rousseeuw, P. J., and Yohai, V. (1984). “Robust Regression by Means of S-Estimators.” In Robust and Nonlinear Time Series Analysis, edited by J. Franke, W. Härdle, and R. D. Martin, 256–274. Vol. 26 of Lecture Notes in Statistics. Berlin: Springer-Verlag.

Tibshirani, R. (1996). “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society, Series B 58:267–288.

Timm, N. H. (2002). Applied Multivariate Analysis. New York: Springer.

Weisberg, S. (1985). Applied Linear Regression. 2nd ed. New York: John Wiley & Sons.

Weisberg, S. (2005). Applied Linear Regression. 3rd ed. New York: John Wiley & Sons.

Yohai, V. J. (1987). “High Breakdown Point and High Efficiency Robust Estimates for Regression.” Annals of Statistics 15:642–656.

Younger, M. S. (1979). Handbook for Linear Regression. North Scituate, MA: Duxbury Press.