Introduction to Power and Sample Size Analysis

Standard Hypothesis Tests

In statistical hypothesis testing, you typically express the belief that some effect exists in a population by specifying an alternative hypothesis 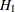$H_1$ . You state a null hypothesis 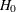$H_0$ as the assertion that the effect does not exist and attempt to gather evidence to reject 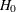$H_0$ in favor of 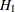$H_1$ . Evidence is gathered in the form of sample data, and a statistical test is used to assess 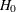$H_0$ . 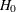If $H_0$ is rejected but there really is no effect, this is called a Type I error. The probability of a Type I error is usually designated "alpha" or $\alpha$ , and statistical tests are designed to ensure that $\alpha$ is suitably small (for example, less than 0.05).

If there is an effect in the population but 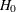$H_0$ is not rejected in the statistical test, then a Type II error has been committed. The probability of a Type II error is usually designated "beta" or 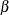$\beta$ . The probability 1 – 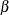$\beta$ of avoiding a Type II error (that is, correctly rejecting 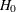$H_0$ and achieving statistical significance) is called the power of the test.

Most, but not all, of the power analyses in the GLMPOWER and POWER procedures are based on such standard hypothesis tests.