Introduction to Statistical Modeling with SAS/STAT Software
Hypothesis Testing and Power
In statistical hypothesis testing, you typically express the belief that some effect exists in a population by specifying
an alternative hypothesis 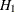 . You state a null hypothesis
. You state a null hypothesis 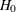 as the assertion that the effect does not exist and attempt to gather evidence to reject
as the assertion that the effect does not exist and attempt to gather evidence to reject 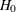 in favor of
in favor of 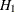 . Evidence is gathered in the form of sample data, and a statistical test is used to assess
. Evidence is gathered in the form of sample data, and a statistical test is used to assess 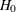 . If
. If 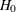 is rejected but there really is no effect, this is called a Type I error. The probability of a Type I error is usually designated "alpha" or
is rejected but there really is no effect, this is called a Type I error. The probability of a Type I error is usually designated "alpha" or  , and statistical tests are designed to ensure that
, and statistical tests are designed to ensure that  is suitably small (for example, less than 0.05).
is suitably small (for example, less than 0.05).
If there is an effect in the population but 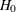 is not rejected in the statistical test, then a Type II error has been committed. The probability of a Type II error is usually designated "beta" or
is not rejected in the statistical test, then a Type II error has been committed. The probability of a Type II error is usually designated "beta" or 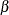 . The probability
. The probability 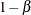 of avoiding a Type II error—that is, correctly rejecting
of avoiding a Type II error—that is, correctly rejecting 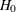 and achieving statistical significance, is called the power of the test.
and achieving statistical significance, is called the power of the test.
An important goal in study planning is to ensure an acceptably high level of power. Sample size plays a prominent role in power computations because the focus is often on determining a sufficient sample size to achieve a certain power, or assessing the power for a range of different sample sizes.
There are several tools available in SAS/STAT software for power and sample size analysis. PROC POWER covers a variety of analyses such as t tests, equivalence tests, confidence intervals, binomial proportions, multiple regression, one-way ANOVA, survival analysis, logistic regression, and the Wilcoxon rank-sum test. PROC GLMPOWER supports more complex linear models. The Power and Sample Size application provides a user interface and implements many of the analyses supported in the procedures.