Introduction to Statistical Modeling with SAS/STAT Software
Inference Principles for Survey Data
Design-based and model-assisted statistical inference for survey data requires that the randomness due to the selection mechanism be taken into account. This can require special estimation principles and techniques.
The SURVEYMEANS, SURVEYFREQ, SURVEYREG, SURVEYLOGISTIC, and SURVEYPHREG procedures support design-based and/or model-assisted
inference for sample surveys. Suppose 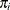 is the selection probability for unit i in sample S. The inverse of the inclusion probability is known as sampling weight and is denoted by
is the selection probability for unit i in sample S. The inverse of the inclusion probability is known as sampling weight and is denoted by 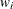 . Briefly, the idea is to apply a relationship that exists in the population to the sample and to take into account the sampling
weights. For example, to estimate the finite population total
. Briefly, the idea is to apply a relationship that exists in the population to the sample and to take into account the sampling
weights. For example, to estimate the finite population total 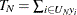 based on the sample S, you can accumulate the sampled values while properly weighting:
based on the sample S, you can accumulate the sampled values while properly weighting: 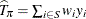 . It is easy to verify that
. It is easy to verify that 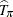 is design-unbiased in the sense that
is design-unbiased in the sense that ![$\mr{E}[\widehat{T}_{\pi } | {\mathcal F}_ N] = T_ N$](images/statug_intromod0139.png) (see Cochran 1977).
(see Cochran 1977).
When a statistical model is present, similar ideas apply. For example, if 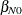 and
and 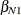 are finite population quantities for a simple linear regression working model that minimize the sum of squares
are finite population quantities for a simple linear regression working model that minimize the sum of squares
![\[ \sum _{i \in U_ N} \left(y_ i - \beta _{0N} - \beta _{1N}x_ i\right)^2 \]](images/statug_intromod0142.png)
in the population, then the sample-based estimators 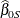 and
and 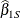 are obtained by minimizing the weighted sum of squares
are obtained by minimizing the weighted sum of squares
![\[ \sum _{i \in S} w_ i (y_ i - \hat\beta _{0S} - \hat\beta _{1S}x_ i)^2 \]](images/statug_intromod0145.png)
in the sample, taking into account the inclusion probabilities.
In model-assisted inference, weighted least squares or pseudo-maximum likelihood estimators are commonly used to solve such estimation problems. Maximum pseudo-likelihood or weighted maximum likelihood estimators for survey data maximize a sample-based estimator of the population likelihood. Assume a working model with uncorrelated responses such that the finite population log-likelihood is
![\[ \sum _{i \in U_ N} l(\theta _{1N}, \ldots , \theta _{pN}; y_ i), \]](images/statug_intromod0146.png)
where 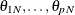 are finite population quantities. For independent sampling, one possible sample-based estimator of the population log likelihood
is
are finite population quantities. For independent sampling, one possible sample-based estimator of the population log likelihood
is
![\[ \sum _{i \in S} w_ i l(\theta _{1N}, \ldots , \theta _{pN}; y_ i) \]](images/statug_intromod0148.png)
Sample-based estimators  are obtained by maximizing this expression.
are obtained by maximizing this expression.
Design-based and model-based statistical analysis might employ the same statistical model (for example, a linear regression) and the same estimation principle (for example, weighted least squares), and arrive at the same estimates. The design-based estimation of the precision of the estimators differs from the model-based estimation, however. For complex surveys, design-based variance estimates are in general different from their model-based counterpart. The SAS/STAT procedures for survey data (SURVEYMEANS, SURVEYFREQ, SURVEYREG, SURVEYLOGISTIC, and SURVEYPHREG procedures) compute design-based variance estimates for complex survey data. See the section Variance Estimation, in Chapter 14: Introduction to Survey Sampling and Analysis Procedures, for details about design-based variance estimation.