Introduction to Mixed Modeling Procedures

Models for Clustered and Hierarchical Data

Mixed models are often applied in situations where data are clustered, grouped, or otherwise hierarchically organized. For example, observations might be collected by randomly selecting schools in a school district, then randomly selecting classrooms within schools, and then randomly selecting students within the classroom. A longitudinal study might randomly select individuals and then repeatedly take measurements on them. In the first example, a school is a cluster of observations, which consists of smaller clusters (classrooms) and so on. In the longitudinal example the observations for a particular individual form a cluster. Mixed models are popular analysis tools for hierarchically organized data for the following reasons:

  • The selection of groups is often performed randomly, so that the associated effects are random effects.

  • The data from different clusters are independent by virtue of the random selection or by assumption.

  • The observations from the same cluster are often correlated, such as the repeated observations in a repeated measures or longitudinal study.

  • It is often believed that there is heterogeneity in model parameters across subjects; for example, slopes and intercepts might differ across individuals in a longitudinal growth study. This heterogeneity, if due to stochastic sources, can be modeled with random effects.

A linear mixed models with clustered, hierarchical structure can be written as a special case of the general linear mixed model by introducing appropriate subscripts. For example, a mixed model with one type of clustering and s clusters can be written as

\[ \bY _ i = \bX _ i\bbeta + \bZ _ i\bgamma _ i + \bepsilon _ i \quad i=1,\ldots ,s \]

In SAS/STAT software, the clusters are referred to as subjects, and the effects that define clusters in your data can be specified with the SUBJECT= option in the GLIMMIX, HPMIXED, MIXED, and NLMIXED procedures. The vector 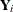$\bY _ i$ collects the 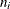$n_ i$ observations for the ith subject. In certain disciplines, the organization of a hierarchical model is viewed in a bottom-up form, where the measured observations represent the first level, these are collected into units at the second level, and so forth. In the school data example, the bottom-up approach considers a student’s score as the level-1 observation, the classroom as the level-2 unit, and the school district as the level-3 unit (if these were also selected from a population of districts).

The following points are noteworthy about mixed models with SUBJECT= specification:

  • A SUBJECT= option is available in the RANDOM statements of the GLIMMIX, HPMIXED, MIXED, and NLMIXED procedures and in the REPEATED statement of the MIXED and HPMIXED procedures.

  • A SUBJECT= specification is required in the NLMIXED and HPMIXED procedures. It is not required with any other mixed modeling procedure in SAS/STAT software.

  • Specifying models with subjects is usually more computationally efficient in the MIXED and GLIMMIX procedures, especially if the SUBJECT= effects are identical or contained within each other. The computational efficiency of the HPMIXED procedure is not dependent on SUBJECT= effects in the manner in which the MIXED and GLIMMIX procedures are affected.

  • There is no limit to the number of SUBJECT= effects with the MIXED, HPMIXED, and GLIMMIX procedures—that is, you can achieve an arbitrary depth of the nesting.