The Four Types of Estimable Functions
General Form of an Estimable Function
This section demonstrates a shorthand technique for displaying the generating set for any estimable  . Suppose
. Suppose
![\[ \mb{X} = \left[ \begin{array}{cccc} 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \end{array} \right] ~ ~ \mbox{ and } ~ ~ \bbeta = \left[ \begin{array}{c} \mu \\ A_1 \\ A_2 \\ A_3 \end{array} \right] \]](images/statug_introglmest0020.png)
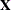 is a generating set for
is a generating set for  , but so is the smaller set
, but so is the smaller set
![\[ \mb{X^*} = \left[ \begin{array}{cccc} 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ \end{array} \right] \]](images/statug_introglmest0021.png)
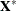 is formed from
is formed from 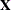 by deleting duplicate rows.
by deleting duplicate rows.
Since all estimable  s must be linear functions of the rows of
s must be linear functions of the rows of 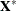 for
for 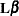 to be estimable, an
to be estimable, an  for a single-degree-of-freedom estimate can be represented symbolically as
for a single-degree-of-freedom estimate can be represented symbolically as
![\[ \mathit{L1} \times (1~ 1~ 0~ 0) + \mathit{L2} \times (1~ 0~ 1~ 0) + \mathit{L3} \times (1~ 0~ 0~ 1) \]](images/statug_introglmest0023.png)
or
![\[ \mb{L} = (\mathit{L1}+\mathit{L2}+\mathit{L3},~ \mathit{L1},~ \mathit{L2},~ \mathit{L3}) ~ \]](images/statug_introglmest0024.png)
For this example, 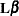 is estimable if and only if the first element of
is estimable if and only if the first element of  is equal to the sum of the other elements of
is equal to the sum of the other elements of  or if
or if
![\[ \mb{L} \bbeta = (\mathit{L1}+\mathit{L2}+\mathit{L3}) \times \mu + \mathit{L1} \times A_1 + \mathit{L2} \times A_2 + \mathit{L3} \times A_3 \]](images/statug_introglmest0025.png)
is estimable for any values of L1, L2, and L3.
If other generating sets for  are represented symbolically, the symbolic notation looks different. However, the inherent nature of the rules is the same.
For example, if row operations are performed on
are represented symbolically, the symbolic notation looks different. However, the inherent nature of the rules is the same.
For example, if row operations are performed on  to produce an identity matrix in the first
to produce an identity matrix in the first  submatrix of the resulting matrix
submatrix of the resulting matrix
![\[ \mb{X^{**}} = \left[ \begin{array}{rrrr} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{array} \right] \]](images/statug_introglmest0027.png)
then 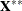 is also a generating set for
is also a generating set for  . An estimable
. An estimable  generated from
generated from 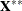 can be represented symbolically as
can be represented symbolically as
![\[ \mb{L} = (\mathit{L1},~ \mathit{L2},~ \mathit{L3},~ \mathit{L1}-\mathit{L2}-\mathit{L3}) ~ \]](images/statug_introglmest0029.png)
Note that, again, the first element of  is equal to the sum of the other elements.
is equal to the sum of the other elements.
With multiple generating sets available, the question arises as to which one is the best to represent  symbolically. Clearly, a generating set containing a minimum of rows (of full row rank) and a maximum of zero elements is
desirable.
symbolically. Clearly, a generating set containing a minimum of rows (of full row rank) and a maximum of zero elements is
desirable.
The generalized 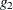 -inverse
-inverse 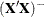 of
of 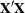 computed by the modified sweep operation (Goodnight 1979) has the property that
computed by the modified sweep operation (Goodnight 1979) has the property that 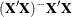 usually contains numerous zeros. For this reason, in PROC GLM the nonzero rows of
usually contains numerous zeros. For this reason, in PROC GLM the nonzero rows of 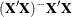 are used to represent
are used to represent  symbolically.
symbolically.
If the generating set represented symbolically is of full row rank, the number of symbols 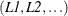 represents the maximum rank of any testable hypothesis (in other words, the maximum number of linearly independent rows for
any
represents the maximum rank of any testable hypothesis (in other words, the maximum number of linearly independent rows for
any  matrix that can be constructed). By letting each symbol in turn take on the value of 1 while the others are set to 0, the
original generating set can be reconstructed.
matrix that can be constructed). By letting each symbol in turn take on the value of 1 while the others are set to 0, the
original generating set can be reconstructed.