Introduction to Clustering Procedures
Multinormal Clusters of Unequal Size and Dispersion
In this example, there are three multinormal clusters that differ in size and dispersion. PROC FASTCLUS and five of the hierarchical methods available in PROC CLUSTER are used. To help you compare methods, the true, generated clusters are plotted.
The following SAS statements produce Figure 11.10:
data unequal;
keep x y c;
mx=1; my=0; n=20; scale=.5; c=1; link generate;
mx=6; my=0; n=80; scale=2.; c=3; link generate;
mx=3; my=4; n=40; scale=1.; c=2; link generate;
stop;
generate:
do i=1 to n;
x=rannor(1)*scale+mx;
y=rannor(1)*scale+my;
output;
end;
return;
run;
title 'True Clusters for Data Containing Multinormal Clusters of Unequal Size'; proc sgplot; scatter y=y x=x / group=c; run;
Figure 11.10: Generated Clusters of Unequal Size
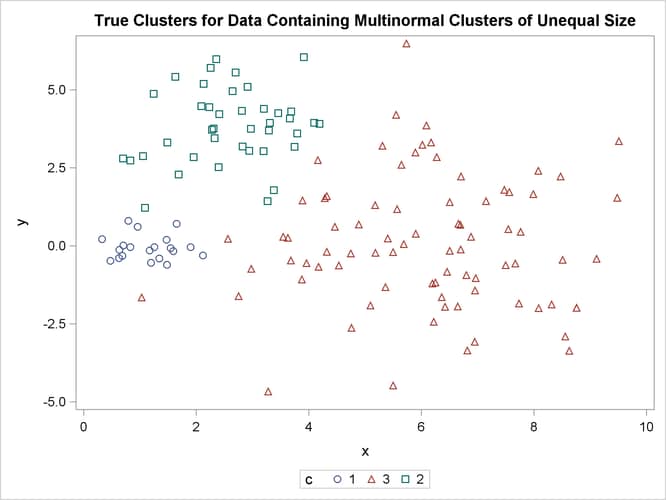
The following statements use the FASTCLUS procedure to find three clusters and then use the SGPLOT procedure to plot the clusters. The following statements produce Figure 11.11:
proc fastclus data=unequal out=out maxc=3 noprint; var x y; title 'FASTCLUS Analysis: Compact Clusters of Unequal Size'; run; proc sgplot; scatter y=y x=x / group=cluster; run;
Figure 11.11: Compact Clusters of Unequal Size: PROC FASTCLUS
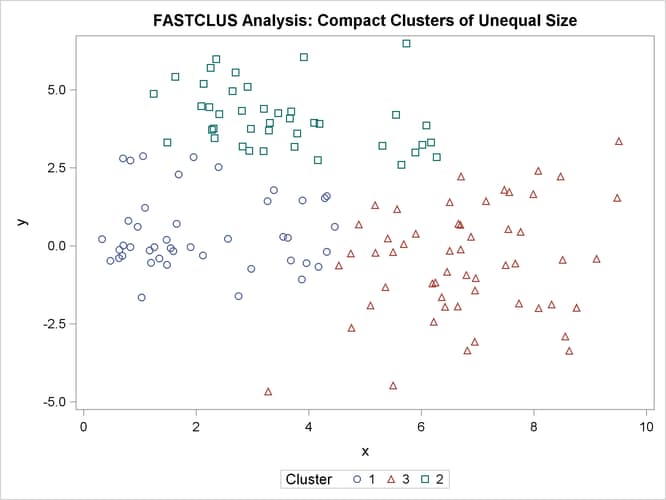
The following SAS statements produce Figure 11.12:
proc cluster data=unequal outtree=tree method=ward noprint;
var x y;
run;
proc tree noprint out=out n=3;
copy x y;
title 'Ward''s Minimum Variance Cluster Analysis: '
'Compact Clusters of Unequal Size';
run;
proc sgplot;
scatter y=y x=x / group=cluster;
run;
Figure 11.12: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=WARD
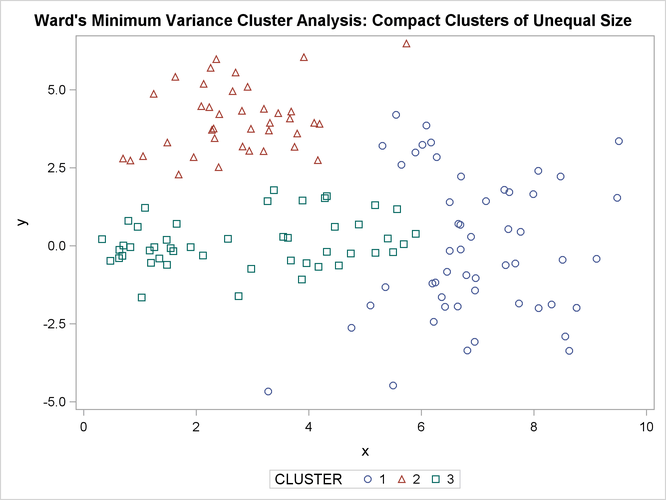
The following SAS statements produce Figure 11.13:
proc cluster data=unequal outtree=tree method=average noprint;
var x y;
run;
proc tree noprint out=out n=3 dock=5;
copy x y;
title 'Average Linkage Cluster Analysis: '
'Compact Clusters of Unequal Size';
run;
proc sgplot;
scatter y=y x=x / group=cluster;
run;
Figure 11.13: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=AVERAGE
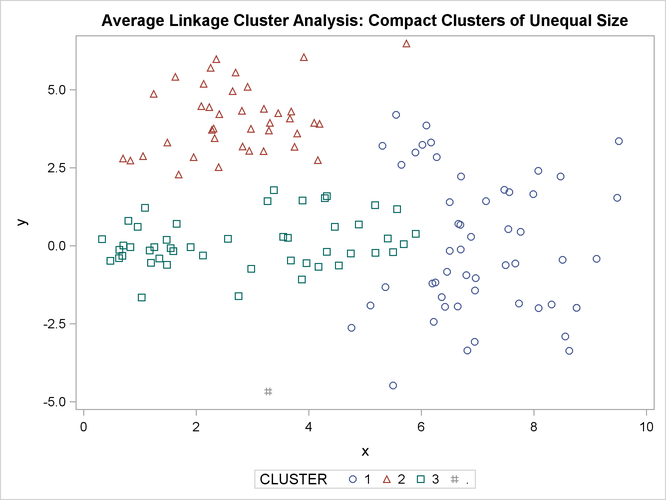
The following SAS statements produce Figure 11.14:
proc cluster data=unequal outtree=tree method=centroid noprint;
var x y;
run;
proc tree noprint out=out n=3 dock=5;
copy x y;
title 'Centroid Cluster Analysis: '
'Compact Clusters of Unequal Size';
run;
proc sgplot;
scatter y=y x=x / group=cluster;
run;
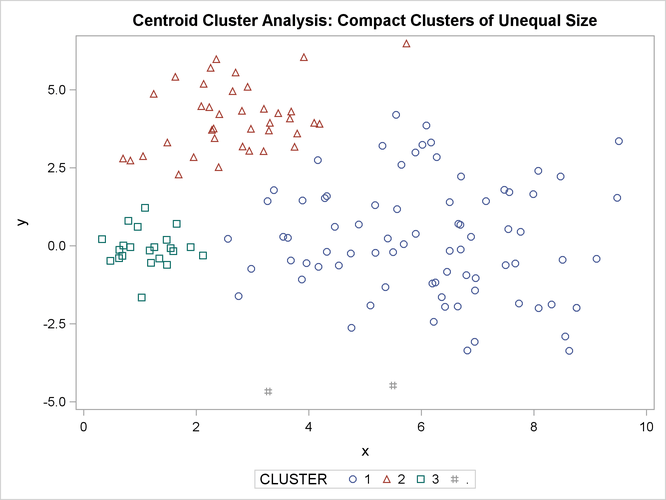
Figure 11.14: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=CENTROID
The following SAS statements produce Figure 11.15 and Figure 11.16:
proc cluster data=unequal outtree=tree method=twostage k=10 noprint;
var x y;
run;
proc tree noprint out=out n=3;
copy x y _dens_;
title 'Two-Stage Density Linkage Cluster Analysis: '
'Compact Clusters of Unequal Size';
run;
proc sgplot;
scatter y=y x=x / group=cluster;
run;
proc sgplot;
bubble y=y x=x size=_dens_ / nofill lineattrs=graphdatadefault;
title 'Estimated Densities for Data Containing '
'Compact Clusters of Unequal Size';
run;
Figure 11.15: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=TWOSTAGE
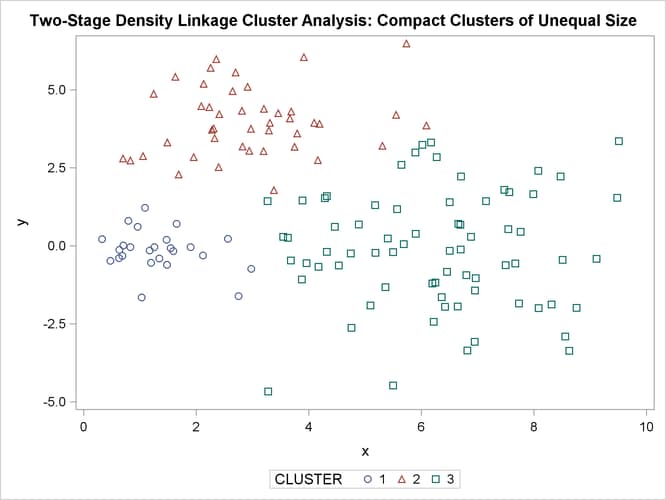
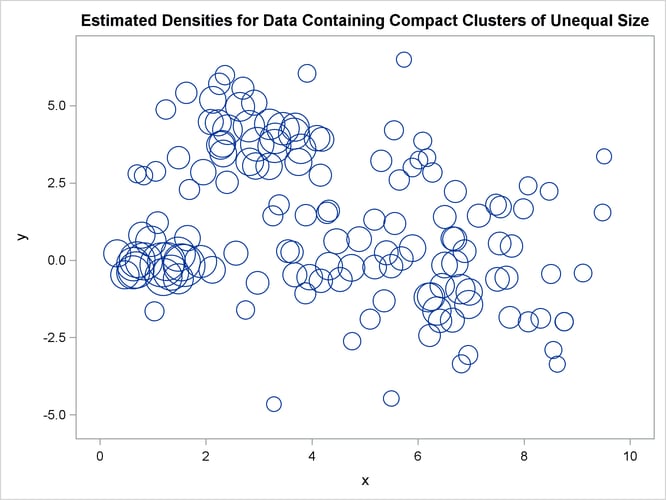
Figure 11.16: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=TWOSTAGE
The following SAS statements produce Figure 11.17:
proc cluster data=unequal outtree=tree method=single noprint;
var x y;
run;
proc tree data=tree noprint out=out n=3 dock=5;
copy x y;
title 'Single Linkage Cluster Analysis: '
'Compact Clusters of Unequal Size';
run;
proc sgplot;
scatter y=y x=x / group=cluster;
run;
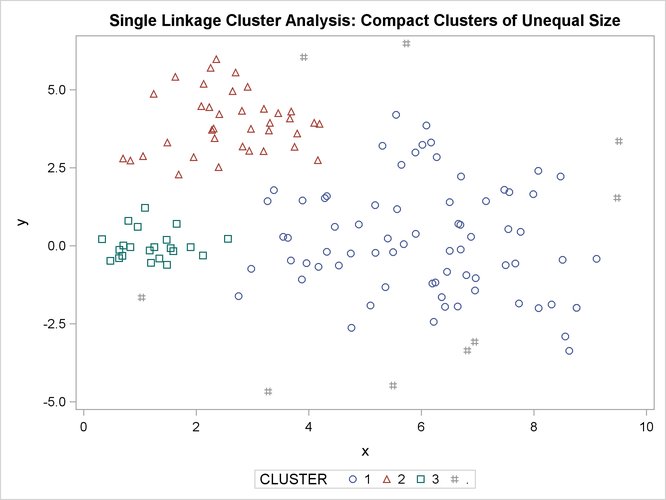
Figure 11.17: Compact Clusters of Unequal Size: PROC CLUSTER METHOD=SINGLE
In the PROC FASTCLUS analysis, the smallest cluster, in the bottom-left portion of the plot, has stolen members from the other two clusters, and the upper-left cluster has also acquired some observations that rightfully belong to the larger, lower-right cluster. With Ward’s method, the upper-left cluster is separated correctly, but the lower-left cluster has taken a large bite out of the lower-right cluster. For both of these methods, the clustering errors are in accord with the biases of the methods to produce clusters of equal size. In the average linkage analysis, both the upper-left and lower-left clusters have encroached on the lower-right cluster, thereby making the variances more nearly equal than in the true clusters. The centroid method, which lacks the size and dispersion biases of the previous methods, obtains an essentially correct partition.
Two-stage density linkage does almost as well, even though the compact shapes of these clusters favor the traditional methods. Single linkage also produces excellent results.