Introduction to Structural Equation Modeling with Latent Variables
Errors-in-Variables Regression
For ordinary unconstrained regression models, there is no reason to use PROC CALIS instead of PROC REG. But suppose that the predictor variable X is a random variable that is contaminated by errors (especially measurement errors), and you want to estimate the linear relationship between the true, error-free scores. The following model takes this kind of measurement errors into account:

The model assumes the following:
![\[ \mbox{Cov}(F_ X,E_ Y) = \mbox{Cov}(F_ X,E_ X) = \mbox{Cov}(E_ X,E_ Y) = 0 \]](images/statug_introcalis0015.png)
There are two equations in the model. The first one is the so-called structural model, which describes the relationships
between Y and the true score predictor  . This equation is your main interest. However,
. This equation is your main interest. However,  is a latent variable that has not been observed. Instead, what you have observed for this predictor is X, which is the contaminated version of
is a latent variable that has not been observed. Instead, what you have observed for this predictor is X, which is the contaminated version of  with measurement error or other errors, denoted by
with measurement error or other errors, denoted by  , added. This measurement process is described in the second equation, or the so-called measurement model. By analyzing the
structural and measurement models (or the two linear equations) simultaneously, you want to estimate the true score effect
, added. This measurement process is described in the second equation, or the so-called measurement model. By analyzing the
structural and measurement models (or the two linear equations) simultaneously, you want to estimate the true score effect
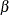 .
.
The assumption that the error terms  and
and 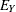 and the latent variable
and the latent variable  are jointly uncorrelated is of critical importance in the model. This assumption must be justified on substantive grounds
such as the physical properties of the measurement process. If this assumption is violated, the estimators might be severely
biased and inconsistent.
are jointly uncorrelated is of critical importance in the model. This assumption must be justified on substantive grounds
such as the physical properties of the measurement process. If this assumption is violated, the estimators might be severely
biased and inconsistent.
You can express the current errors-in-variables model by the LINEQS modeling language as shown in the following statements:
proc calis;
lineqs
Y = beta * Fx + Ey,
X = 1. * Fx + Ex;
run;
In this specification, you need to specify only the equations involved without specifying the assumptions about the correlations
among Fx, Ey, and Ex. In the LINEQS modeling language, you should always name latent factors with the 'F' or 'f' prefix (for example, Fx) and error terms with the 'E' or 'e' prefix (for example, Ey and Ex). Given this LINEQS notation, latent factors and error terms, by default, are uncorrelated in the model.
Consider an example of an errors-in-variables regression model. Fuller (1987, pp. 18–19) analyzes a data set from Voss (1969) that involves corn yields (Y) and available soil nitrogen (X) for which there is a prior estimate of the measurement error for soil nitrogen Var( ) of 57. The scientific question is: how does nitrogen affect corn yields? The linear prediction of corn yields by nitrogen
should be based on a measure of nitrogen that is not contaminated with measurement error. Hence, the errors-in-variables model
is applied.
) of 57. The scientific question is: how does nitrogen affect corn yields? The linear prediction of corn yields by nitrogen
should be based on a measure of nitrogen that is not contaminated with measurement error. Hence, the errors-in-variables model
is applied.  in the model represents the "true" nitrogen measure, X represents the observed measure of nitrogen, which has a true score component
in the model represents the "true" nitrogen measure, X represents the observed measure of nitrogen, which has a true score component  and an error component
and an error component  . Given that the measurement error for soil nitrogen Var(
. Given that the measurement error for soil nitrogen Var( ) is 57, you can specify the errors-in-variables regression model with the following statements in PROC CALIS:
) is 57, you can specify the errors-in-variables regression model with the following statements in PROC CALIS:
data corn(type=cov); input _type_ $ _name_ $ y x; datalines; cov y 87.6727 . cov x 104.8818 304.8545 mean . 97.4545 70.6364 n . 11 11 ;
proc calis data=corn;
lineqs
Y = beta * Fx + Ey,
X = 1. * Fx + Ex;
variance
Ex = 57.;
run;
In the VARIANCE statement, the variance of Ex (measurement error for X) is given as the constant value 57. PROC CALIS produces the estimates shown in Figure 17.4.
Figure 17.4: Errors-in-Variables Model for Corn Data
In Figure 17.4, the estimate of beta is 0.4232 with a standard error estimate of 0.1658. The t value is 2.552. It is significant at the 0.05  -level when compared to the critical value of the standard normal variate (that is, the z table). Also shown in Figure 17.4 are the estimated variances of
-level when compared to the critical value of the standard normal variate (that is, the z table). Also shown in Figure 17.4 are the estimated variances of Fx, Ey, and their estimated standard errors. The names of these parameters have the prefix '_Add'. They are added by PROC CALIS
as default parameters. By employing some conventional rules for setting default parameters, PROC CALIS makes your model specification
much easier and concise. For example, you do not need to specify each error variance parameter manually if it is not constrained
in the model. However, you can specify these parameters explicitly if you desire. Note that in Figure 17.4, the variance of Ex is shown to be 57 without a standard error estimate because it is a fixed constant in the model.
What if you did not model the measurement error in the predictor X? That is, what is the estimate of beta if you use ordinary regression of Y on X, as described by the equation in the section Simple Linear Regression? You can specify such a linear regression model easily by the LINEQS modeling language. Here, you specify this linear regression
model as a special case of the errors-in-variables model. That is, you constrain the variance of measurement error  to 0 in the preceding LINEQS model specification to form the linear regression model, as shown in the following statements:
to 0 in the preceding LINEQS model specification to form the linear regression model, as shown in the following statements:
proc calis data=corn;
lineqs
Y = beta * Fx + Ey,
X = 1. * Fx + Ex;
variance
Ex = 0.;
run;
Fixing the variance of Ex to zero forces the equality of X and  in the measurement model so that this "new" errors-in-variables model is in fact an ordinary regression model. PROC CALIS
produces the estimation results in Figure 17.5.
in the measurement model so that this "new" errors-in-variables model is in fact an ordinary regression model. PROC CALIS
produces the estimation results in Figure 17.5.
Figure 17.5: Ordinary Regression Model for Corn Data: Zero Measurement Error in X
The estimate of beta is now 0.3440, which is an underestimate of the effect of nitrogen on corn yields given the presence of nonzero measurement
error in X, where the estimate of beta is 0.4232.