Introduction to Structural Equation Modeling with Latent Variables

Testing Covariance Patterns

Subsections:

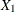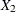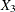The most basic use of PROC CALIS is testing covariance patterns. Consider a repeated-measures experiment where individuals are tested for their motor skills at three different time points. No treatments are introduced between these tests. The three test scores are denoted as $X_1$ , $X_2$ , and $X_3$ , respectively. These test scores are likely correlated because the same set of individuals has been used. More specifically, the researcher wants to test the following pattern of the population covariance matrix 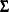$\bSigma$ :

$\bSigma = \left( \begin{array}{ccc} \phi & \theta & \theta \\ \theta & \phi & \theta \\ \theta & \theta & \phi \\ \end{array} \right) \quad$

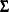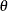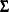Because there are no treatments between the tests, this pattern assumes that the distribution of motor skills stays more or less the same over time, as represented by the same $\phi$ for the diagonal elements of $\bSigma$ . The covariances between the test scores for motor skills also stay the same, as represented by the same $\theta$ for all the off-diagonal elements of $\bSigma$ .

Suppose you summarize your data in a covariance matrix, which is stored in the following SAS data set:

data motor(type=cov);
   input _type_ $ _name_ $ x1 x2 x3;
   datalines;
COV     x1      3.566   1.342   1.114
COV     x2      1.342   4.012   1.056
COV     x3      1.114   1.056   3.776
N        .         36      36      36
;

The diagonal elements are somewhat close to each other but are not the same. The off-diagonal elements are also very close to each other but are not the same. Could these observed differences be due to chance? Given the sample covariance matrix, can you test the hypothesized patterned covariance matrix in the population?

Setting up this patterned covariance model in PROC CALIS is straightforward with the MSTRUCT modeling language:

proc calis data=motor;
   mstruct var  = x1-x3;
   matrix _cov_ = phi
                  theta phi
                  theta theta phi;
run;

In the VAR= option in the MSTRUCT statement, you specify that x1–x3 are the variables in the covariance matrix. Next, you specify the elements of the patterned covariance matrix in the MATRIX statement with the _COV_ keyword. Because the covariance matrix is symmetric, you need to specify only the lower triangular elements in the MATRIX statement. You use phi for the parameters of all diagonal elements and theta for the parameters of all off-diagonal elements. Matrix elements with the same parameter name are implicitly constrained to be equal. Hence, this is the patterned covariance matrix that you want to test. Some output results from PROC CALIS are shown in Figure 17.1.

Figure 17.1: Fit Summary

Fit Summary
Chi-Square	0.3656
Chi-Square DF	4
Pr > Chi-Square	0.9852

3.7847

0.5701

6.6383

<.0001

[phi]

1.1707

0.5099

2.2960

0.0217

[theta]

1.1707

0.5099

2.2960

0.0217

[theta]

1.1707

0.5099

2.2960

0.0217

[theta]

3.7847

0.5701

6.6383

<.0001

[phi]

1.1707

0.5099

2.2960

0.0217

[theta]

1.1707

0.5099

2.2960

0.0217

[theta]

1.1707

0.5099

2.2960

0.0217

[theta]

3.7847

0.5701

6.6383

<.0001

[phi]

First, PROC CALIS shows that the chi-square test for the model fit is 0.3656 (df = 4, p=0.9852). Because the chi-square test is not significant, it supports the hypothesized patterned covariance model. Next, PROC CALIS shows the estimates in the covariance matrix under the hypothesized model. The estimates for the diagonal elements are all 3.7847, and the estimates for off-diagonal elements are all 1.1707. Estimates of standard errors and t values for these covariance and variance parameters are also shown.

The MSTRUCT modeling language in PROC CALIS enables you to test various kinds of covariance and mean patterns, including matrices with fixed or constrained values. For example, consider a population covariance model in which correlations among the motor test scores are hypothesized to be zero. In other words, the covariance pattern is:

$\bSigma = \left( \begin{array}{ccc} \phi _1 & 0 & 0 \\ 0 & \phi _2 & 0 \\ 0 & 0 & \phi _3 \\ \end{array} \right) \quad$

Essentially, this diagonally-patterned covariance model means that the data are randomly and independently generated for x1–x3 under the multivariate normal distribution. Only the variances of the variables are parameters in the model, and the variables are not correlated at all.

You can use the MSTRUCT modeling language of PROC CALIS to fit this diagonally-patterned covariance matrix to the data for motor skills, as shown in the following statements:

proc calis data=motor;
   mstruct var  = x1-x3;
   matrix _cov_ = phi1
                     0.   phi2
                     0.      0.    phi3;
run;

Some of the output is shown in Figure 17.2.

Figure 17.2: Fit Summary: Testing Uncorrelatedness

Fit Summary
Chi-Square	9.2939
Chi-Square DF	3
Pr > Chi-Square	0.0256

3.5660

0.8524

4.1833

<.0001

[phi1]

4.0120

0.9591

4.1833

<.0001

[phi2]

3.7760

0.9026

4.1833

<.0001

[phi3]

PROC CALIS shows that the chi-square test for the model fit is 9.2939 (df=3, p=0.0256). Because the chi-square test is significant, it does not support the patterned covariance model that postulates zero correlations among the variables. This conclusion is consistent with what is already known—the motor test scores should be somewhat correlated because they are measurements over time for the same group of individuals.

The output also shows the estimates of variances under the model. Each diagonal element of the covariance matrix has a distinct estimate because different parameters have been hypothesized under the patterned covariance model.