The TTEST Procedure
Define the following notation:

The mean estimate ![]() , standard deviation estimate s, and standard error
, standard deviation estimate s, and standard error ![]() are computed as follows:
are computed as follows:
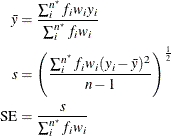
The 100(1 – ![]() )% confidence interval for the mean
)% confidence interval for the mean ![]() is
is
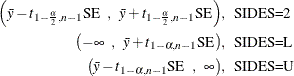
The t value for the test is computed as
The p-value of the test is computed as
![\[ p\mbox{-value} = \left\{ \begin{array}{ll} P \left( t^2 > F_{1-\alpha , 1, n-1} \right) \; \; , & \mbox{2-sided} \\ P \left( t < t_{\alpha , n-1} \right) \; \; , & \mbox{lower 1-sided} \\ P \left( t > t_{1-\alpha , n-1} \right) \; \; , & \mbox{upper 1-sided} \\ \end{array} \right. \]](images/statug_ttest0032.png)
The equal-tailed confidence interval for the standard deviation (CI=
EQUAL) is based on the acceptance region of the test of ![]() that places an equal amount of area (
that places an equal amount of area (![]() ) in each tail of the chi-square distribution:
) in each tail of the chi-square distribution:
The acceptance region can be algebraically manipulated to give the following 100(1 – ![]() )% confidence interval for
)% confidence interval for ![]() :
:
![\[ \left(\frac{(n-1)s^2}{\chi _{1-\frac{\alpha }{2},n-1}^2} \; \; , \; \; \frac{(n-1)s^2}{\chi _{\frac{\alpha }{2},n-1}^2}\right) \]](images/statug_ttest0035.png)
Taking the square root of each side yields the 100(1 – ![]() )% CI=
EQUAL confidence interval for
)% CI=
EQUAL confidence interval for ![]() :
:
![\[ \left(\left(\frac{(n-1)s^2}{\chi _{1-\frac{\alpha }{2},n-1}^2}\right)^\frac {1}{2} \; \; , \; \; \left( \frac{(n-1)s^2}{\chi _{\frac{\alpha }{2},n-1}^2} \right)^\frac {1}{2} \right) \]](images/statug_ttest0036.png)
The other confidence interval for the standard deviation (CI=
UMPU) is derived from the uniformly most powerful unbiased test of ![]() (Lehmann, 1986). This test has acceptance region
(Lehmann, 1986). This test has acceptance region
where the critical values ![]() and
and ![]() satisfy
satisfy
and
where ![]() is the PDF of the chi-square distribution with
is the PDF of the chi-square distribution with ![]() degrees of freedom. This acceptance region can be algebraically manipulated to arrive at
degrees of freedom. This acceptance region can be algebraically manipulated to arrive at
where ![]() and
and ![]() solve the preceding two integrals. To find the area in each tail of the chi-square distribution to which these two critical
values correspond, solve
solve the preceding two integrals. To find the area in each tail of the chi-square distribution to which these two critical
values correspond, solve ![]() and
and ![]() for
for ![]() and
and ![]() ; the resulting
; the resulting ![]() and
and ![]() sum to
sum to ![]() . Hence, a 100(1 –
. Hence, a 100(1 – ![]() )% confidence interval for
)% confidence interval for ![]() is given by
is given by
Taking the square root of each side yields the 100(1 – ![]() )% CI=
UMPU confidence interval for
)% CI=
UMPU confidence interval for ![]() :
:
![\[ \left(\left( \frac{(n-1)s^2}{\chi _{1-\alpha _2,n-1}^2} \right)^\frac {1}{2} \; \; , \; \; \left(\frac{(n-1)s^2}{\chi _{\alpha _1,n-1}^2} \right)^\frac {1}{2} \right) \]](images/statug_ttest0049.png)
The DIST= LOGNORMAL analysis is handled by log-transforming the data and null value, performing a DIST= NORMAL analysis, and then transforming the results back to the original scale. This simple technique is based on the properties of the lognormal distribution as discussed in Johnson, Kotz, and Balakrishnan (1994, Chapter 14).
Taking the natural logarithms of the observation values and the null value, define
First, a DIST=
NORMAL analysis is performed on ![]() with the null value
with the null value ![]() , producing the mean estimate
, producing the mean estimate ![]() , the standard deviation estimate
, the standard deviation estimate ![]() , a t value, and a p-value. The geometric mean estimate
, a t value, and a p-value. The geometric mean estimate ![]() and the CV estimate
and the CV estimate ![]() of the original lognormal data are computed as follows:
of the original lognormal data are computed as follows:
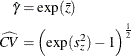
The t value and p-value remain the same. The confidence limits for the geometric mean and CV on the original lognormal scale are computed from
the confidence limits for the arithmetic mean and standard deviation in the DIST=
NORMAL analysis on the log-transformed data, in the same way that ![]() is derived from
is derived from ![]() and
and ![]() is derived from
is derived from ![]() .
.
