The POWER Procedure
- Overview
-
Getting Started

-
Syntax

-
Details

-
Examples
 One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test
One-Way ANOVAThe Sawtooth Power Function in Proportion AnalysesSimple AB/BA Crossover DesignsNoninferiority Test with Lognormal DataMultiple Regression and CorrelationComparing Two Survival CurvesConfidence Interval PrecisionCustomizing PlotsBinary Logistic Regression with Independent PredictorsWilcoxon-Mann-Whitney Test - References
Consider the following plot request for a sample size analysis similar to the one in Output 77.8.1 but with only a single scenario, and with unbalanced sample size allocation of 2:1:
proc power plotonly;
ods output plotcontent=PlotData;
twosamplemeans test=diff
groupmeans = 12 | 18
stddev = 7
groupweights = 2 | 1
power = .
ntotal = 20;
plot x=n min=20 max=50 npoints=20;
run;
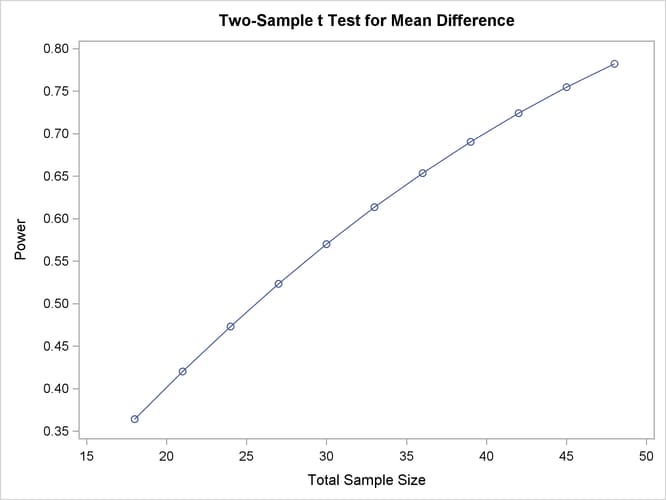
The MIN= , MAX= , and NPOINTS= options in the PLOT statement request a plot with 20 points between 20 and 50. But the resulting plot (Output 77.8.7) appears to have only 11 points, and they range from 18 to 48.
The reason that this plot has fewer points than usual is due to the rounding of sample sizes. If you do not use the NFRACTIONAL
option in the analysis statement (here, the TWOSAMPLEMEANS
statement), then the set of sample size points determined by the MIN=
, MAX=
, NPOINTS=
, and STEP=
options in the PLOT
statement can be rounded to satisfy the allocation weights. In this case, they are rounded down to the nearest multiples
of 3 (the sum of the weights), and many of the points overlap. To see the overlap, you can print the NominalNTotal (unadjusted) and NTotal (rounded) variables in the PlotContent ODS object (here saved to a data set called PlotData):
proc print data=PlotData; var NominalNTotal NTotal; run;
The output is shown in Output 77.8.8.
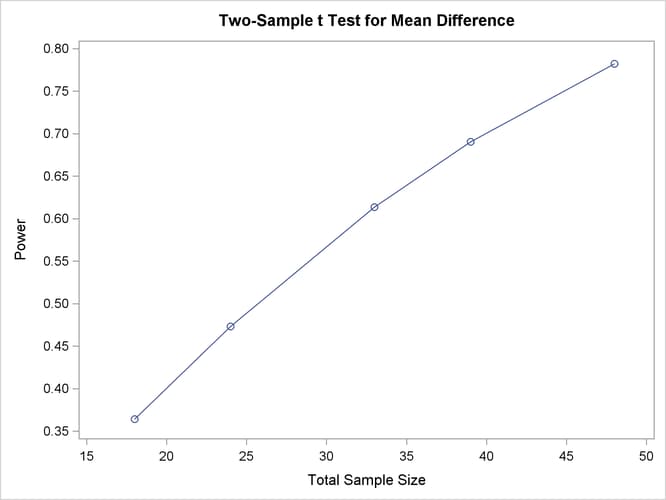
Besides overlapping of sample size points, another peculiarity that might occur without the NFRACTIONAL option is unequal spacing—for example, in the plot in Output 77.8.9, created with the following statements:
proc power plotonly;
twosamplemeans test=diff
groupmeans = 12 | 18
stddev = 7
groupweights = 2 | 1
power = .
ntotal = 20;
plot x=n min=20 max=50 npoints=5;
run;
If you want to guarantee evenly spaced, nonoverlapping sample size points in your plots, you can either (1) use the NFRACTIONAL option in the analysis statement preceding the PLOT statement or (2) use the STEP= option and provide values for the MIN= , MAX= , and STEP= options in the PLOT statement that are multiples of the sum of the allocation weights. Note that this sum is simply 1 for one-sample and paired designs and 2 for balanced two-sample designs. So any integer step value works well for one-sample and paired designs, and any even step value works well for balanced two-sample designs. Both of these strategies will avoid rounding adjustments.
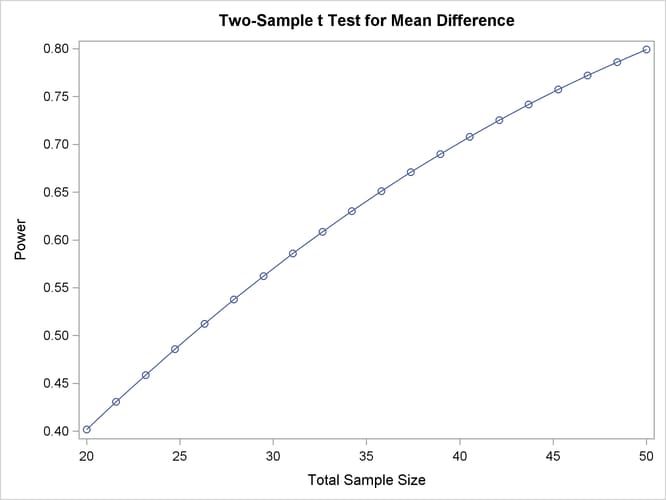
The following statements implement the first strategy to create the plot in Output 77.8.10, by using the NFRACTIONAL option in the TWOSAMPLEMEANS statement:
proc power plotonly;
twosamplemeans test=diff
nfractional
groupmeans = 12 | 18
stddev = 7
groupweights = 2 | 1
power = .
ntotal = 20;
plot x=n min=20 max=50 npoints=20;
run;
To implement the second strategy, use multiples of 3 for the STEP= , MIN= , and MAX= options in the PLOT statement (because the sum of the allocation weights is 2 + 1 = 3). The following statements use STEP= 3, MIN= 18, and MAX= 48 to create a plot that looks identical to the plot in Output 77.8.7 but suffers no overlapping of points:
proc power plotonly;
twosamplemeans test=diff
groupmeans = 12 | 18
stddev = 7
groupweights = 2 | 1
power = .
ntotal = 20;
plot x=n min=18 max=48 step=3;
run;