The POWER Procedure

Analyses in the ONEWAYANOVA Statement

One-Degree-of-Freedom Contrast (TEST=CONTRAST)

The hypotheses are

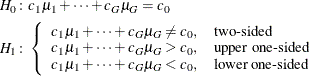
\begin{align*} H_{0}\colon & c_1 \mu _1 + \cdots + c_ G \mu _ G = c_0 \\ H_{1}\colon & \left\{ \begin{array}{ll} c_1 \mu _1 + \cdots + c_ G \mu _ G \ne c_0, & \mbox{two-sided} \\ c_1 \mu _1 + \cdots + c_ G \mu _ G > c_0, & \mbox{upper one-sided} \\ c_1 \mu _1 + \cdots + c_ G \mu _ G < c_0, & \mbox{lower one-sided} \\ \end{array} \right. \\ \end{align*}

where G is the number of groups, $\{ c_1, \ldots , c_ G\} $ are the contrast coefficients, and $c_0$ is the null contrast value.

The test is the usual F test for a contrast in one-way ANOVA. It assumes normal data with common group variances and requires $N \ge G+1$ and $n_ i \ge 1$.

O’Brien and Muller (1993, Section 8.2.3.2) give the exact power as

\[ \mr{power} = \left\{ \begin{array}{ll} P\left(F(1, N-G, \delta ^2) \ge F_{1-\alpha }(1, N-G)\right), & \mbox{two-sided} \\ P\left(t(N-G, \delta ) \ge t_{1-\alpha }(N-G)\right), & \mbox{upper one-sided} \\ P\left(t(N-G, \delta ) \le t_{\alpha }(N-G)\right), & \mbox{lower one-sided} \\ \end{array} \right. \]

where

\[ \delta = N^\frac {1}{2} \left( \frac{\sum _{i=1}^{G} c_ i \mu _ i - c_0}{\sigma \left( \sum _{i=1}^{G} \frac{c_ i^2}{w_ i} \right)^\frac {1}{2}} \right) \]
Overall F Test (TEST=OVERALL)

The hypotheses are

\begin{align*} H_{0}\colon & \mu _1 = \mu _2 = \cdots = \mu _ G \\ H_{1}\colon & \mu _ i \ne \mu _ j \mbox{ for some } i,j \\ \end{align*}

where G is the number of groups.

The test is the usual overall F test for equality of means in one-way ANOVA. It assumes normal data with common group variances and requires $N \ge G+1$ and $n_ i \ge 1$.

O’Brien and Muller (1993, Section 8.2.3.1) give the exact power as

\[ \mr{power} = P\left(F(G-1, N-G, \lambda ) \ge F_{1-\alpha }(G-1, N-G)\right) \]

where the noncentrality is

\[ \lambda = N \left( \frac{\sum _{i=1}^{G} w_ i (\mu _ i - \bar{\mu })^2}{\sigma ^2} \right) \]

and

\[ \bar{\mu } = \sum _{i=1}^{G} w_ i \mu _ i \]