The POWER Procedure

Analyses in the ONECORR Statement

Fisher’s z Test for Pearson Correlation (TEST=PEARSON DIST=FISHERZ)

Fisher’s z transformation (Fisher, 1921) of the sample correlation $R_{Y|(X_1,X_{-1})}$ is defined as

\[ z = \frac{1}{2} \log \left( \frac{1+R_{Y|(X_1,X_{-1})}}{1-R_{Y|(X_1,X_{-1})}} \right) \]

Fisher’s z test assumes the approximate normal distribution $N(\mu , \sigma ^2)$ for z, where

\[ \mu = \frac{1}{2} \log \left( \frac{1+\rho _{Y|(X_1,X_{-1})}}{1-\rho _{Y|(X_1,X_{-1})}} \right) + \frac{\rho _{Y|(X_1,X_{-1})}}{2(N - 1 - p^\star )} \]

and

\[ \sigma ^2 = \frac{1}{N-3-p^\star } \]

where $p^\star $ is the number of variables partialed out (Anderson, 1984, pp. 132–133) and $\rho _{Y|(X_1,X_{-1})}$ is the partial correlation between Y and $X_1$ adjusting for the set of zero or more variables $X_{-1}$.

The test statistic

\[ z^\star = (N-3-p^\star )^{\frac{1}{2}}\left[ z - \frac{1}{2} \log \left( \frac{1+\rho _0}{1-\rho _0} \right) - \frac{\rho _0}{2(N - 1 - p^\star )} \right] \]

is assumed to have a normal distribution $N(\delta , \nu )$, where $\rho _0$ is the null partial correlation and $\delta $ and $\nu $ are derived from Section 16.33 of Stuart and Ord (1994):

\begin{align*} \delta & = (N-3-p^\star )^{\frac{1}{2}} \left[ \frac{1}{2} \log \left( \frac{1+\rho _{Y|(X_1,X_{-1})}}{1-\rho _{Y|(X_1,X_{-1})}} \right) + \frac{\rho _{Y|(X_1,X_{-1})}}{2(N - 1 - p^\star )} \left( 1 + \frac{5 + \rho ^2_{Y|(X_1,X_{-1})}}{4(N - 1 - p^\star )} + \right. \right. \\ & \quad \left. \left. \frac{11 + 2 \rho ^2_{Y|(X_1,X_{-1})} + 3 \rho ^4_{Y|(X_1,X_{-1})}}{8(N - 1 - p^\star )^2} \right) - \frac{1}{2} \log \left( \frac{1+\rho _0}{1-\rho _0} \right) - \frac{\rho _0}{2(N - 1 - p^\star )} \right] \\ \nu & = \frac{N-3-p^\star }{N-1-p^\star } \left[ 1 + \frac{4 - \rho ^2_{Y|(X_1,X_{-1})}}{2(N - 1 - p^\star )} + \frac{22 - 6 \rho ^2_{Y|(X_1,X_{-1})} - 3 \rho ^4_{Y|(X_1,X_{-1})}}{6(N - 1 - p^\star )^2} \right] \\ \end{align*}

The approximate power is computed as

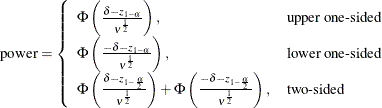
\begin{align*} \mr{power} & = \left\{ \begin{array}{ll} \Phi \left( \frac{\delta - z_{1-\alpha }}{\nu ^\frac {1}{2}}\right), & \mbox{upper one-sided} \\ \Phi \left( \frac{- \delta - z_{1-\alpha }}{\nu ^\frac {1}{2}} \right), & \mbox{lower one-sided} \\ \Phi \left( \frac{\delta - z_{1-\frac{\alpha }{2}}}{\nu ^\frac {1}{2}} \right) + \Phi \left( \frac{- \delta - z_{1-\frac{\alpha }{2}}}{\nu ^\frac {1}{2}} \right), & \mbox{two-sided} \\ \end{array} \right. \\ \end{align*}

Because the test is biased, the achieved significance level might differ from the nominal significance level. The actual alpha is computed in the same way as the power, except that the correlation $\rho _{Y|(X_1,X_{-1})}$ is replaced by the null correlation $\rho _0$.

t Test for Pearson Correlation (TEST=PEARSON DIST=T)

The two-sided case is identical to multiple regression with an intercept and $p_1 = 1$, which is discussed in the section Analyses in the MULTREG Statement.

Let $p^\star $ denote the number of variables partialed out. For the one-sided cases, the test statistic is

\[ t = (N-2-p^\star )^\frac {1}{2} \frac{R_{Y X_1|X_{-1}}}{\left(1 - R^2_{Y X_1|X_{-1}}\right)^\frac {1}{2}} \]

which is assumed to have a null distribution of $t(N-2-p^\star )$.

If the X and Y variables are assumed to have a joint multivariate normal distribution, then the exact power is given by the following formula:

\begin{align*} \mr{power} & = \left\{ \begin{array}{ll} P\left[ (N-2-p^\star )^\frac {1}{2} \frac{R_{Y X_1|X_{-1}}}{\left(1 - R^2_{Y X_1|X_{-1}}\right)^\frac {1}{2}} \ge t_{1-\alpha }(N-2-p^\star )\right], & \mbox{upper one-sided} \\ P\left[ (N-2-p^\star )^\frac {1}{2} \frac{R_{Y X_1|X_{-1}}}{\left(1 - R^2_{Y X_1|X_{-1}}\right)^\frac {1}{2}} \le t_{\alpha }(N-2-p^\star )\right], & \mbox{lower one-sided} \\ \end{array} \right. \\ & = \left\{ \begin{array}{ll} P\left[ R_{Y|(X_1,X_{-1})} \ge \frac{t_{1-\alpha }(N-2-p^\star )}{\left(t^2_{1-\alpha }(N-2-p^\star ) + N-2-p^\star \right)^\frac {1}{2}} \right], & \mbox{upper one-sided} \\ P\left[ R_{Y|(X_1,X_{-1})} \le \frac{t_{\alpha }(N-2-p^\star )}{\left(t^2_{\alpha }(N-2-p^\star ) + N-2-p^\star \right)^\frac {1}{2}} \right], & \mbox{lower one-sided} \\ \end{array} \right. \\ \end{align*}

The distribution of $R_{Y|(X_1,X_{-1})}$ (given the underlying true correlation $\rho _{Y|(X_1,X_{-1})}$) is given in Chapter 32 of Johnson, Kotz, and Balakrishnan (1995).

If the X variables are assumed to have fixed values, then the exact power is given by the noncentral t distribution $t(N-2-p^\star , \delta )$, where the noncentrality is

\[ \delta = N^\frac {1}{2} \frac{\rho _{Y X_1|X_{-1}}}{\left(1 - \rho ^2_{Y X_1|X_{-1}}\right)^\frac {1}{2}} \]

The power is

\begin{align*} \mr{power} & = \left\{ \begin{array}{ll} P\left(t(N-2-p^\star , \delta ) \ge t_{1-\alpha }(N-2-p^\star )\right), & \mbox{upper one-sided} \\ P\left(t(N-2-p^\star , \delta ) \le t_{\alpha }(N-2-p^\star )\right), & \mbox{lower one-sided} \\ \end{array} \right. \\ \end{align*}