Shared Concepts and Topics
A B-spline basis can be built by starting with a set of Haar basis functions, which are functions that are 1 between adjacent
knots and 0 elsewhere, and then applying a simple linear recursion relationship d times, yielding the ![]() needed basis functions. For the purpose of building the B-spline basis, the n prespecified knots are referred to as internal knots. This construction requires d additional knots, known as boundary knots, to be positioned to the left of the internal knots, and
needed basis functions. For the purpose of building the B-spline basis, the n prespecified knots are referred to as internal knots. This construction requires d additional knots, known as boundary knots, to be positioned to the left of the internal knots, and ![]() boundary knots to be positioned to the right of the internal knots. The actual values of these boundary knots can be arbitrary.
The EFFECT statement provides several methods for placing the needed boundary knots, including the common method of using
repeated values of the data extremes as the boundary knots. The boundary knot placement affects the precise form of the basis
functions that are generated, but it does not affect the following two desirable properties:
boundary knots to be positioned to the right of the internal knots. The actual values of these boundary knots can be arbitrary.
The EFFECT statement provides several methods for placing the needed boundary knots, including the common method of using
repeated values of the data extremes as the boundary knots. The boundary knot placement affects the precise form of the basis
functions that are generated, but it does not affect the following two desirable properties:
-
The B-spline basis functions are nonzero over an interval that spans at most
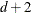 knots. This yields design matrix columns each of whose rows contain at most
knots. This yields design matrix columns each of whose rows contain at most 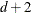 adjacent nonzero entries.
adjacent nonzero entries.
-
The computation of the basis functions at any x value is numerically stable and does not require evaluating powers of this value.
The following figures show the B-spline bases defined on ![]() with four equally spaced internal knots at 0.2, 0.4, 0.6, and 0.8.
with four equally spaced internal knots at 0.2, 0.4, 0.6, and 0.8.
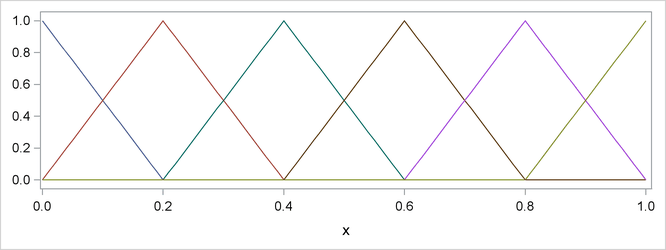
Figure 19.2 shows a linear B-spline basis. Note that this basis consists of six functions each of which is nonzero over an interval that spans at most three knots.
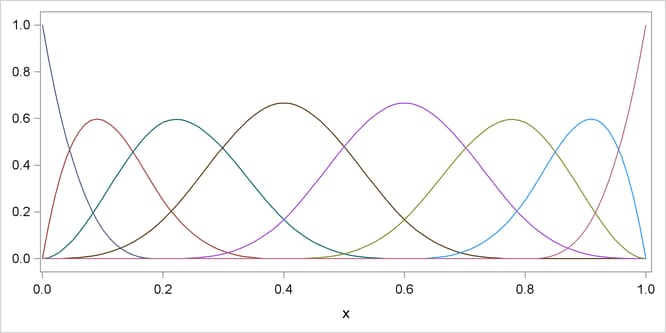
Figure 19.3 shows a cubic B-spline basis where the needed boundary knots are positioned at x = 0 and x = 1. Note that this basis consists of eight functions, each of which is nonzero over an interval spanning at most five knots.
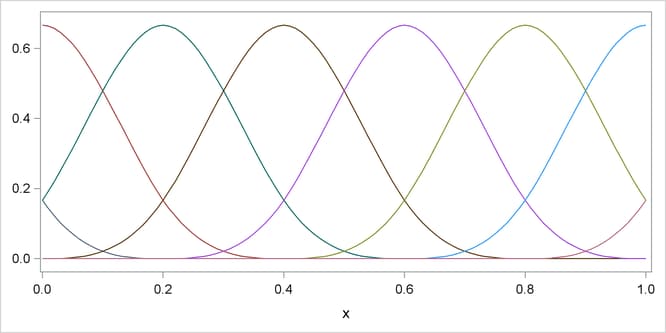
Figure 19.4 shows a different cubic B-spline basis where the needed left-side boundary knots are positioned at –0.6, –0.4, –0.2, and 0. The right-side boundary knots are positioned at 1, 1.2, 1.4, and 1.6. Note that, as in the basis shown in Figure 19.3, this basis consists of eight functions, each of which is nonzero over an interval spanning at most five knots. The different positioning of the boundary knots has merely changed the shape of the individual basis functions.
You can find details about this construction in Hastie, Tibshirani, and Friedman (2001).