Introduction to Clustering Procedures
In this example, the data are sampled from two highly elongated multinormal distributions with equal covariance matrices. The following SAS statements produce Figure 11.18:
data elongate;
keep x y;
ma=8; mb=0; link generate;
ma=6; mb=8; link generate;
stop;
generate:
do i=1 to 50;
a=rannor(7)*6+ma;
b=rannor(7)+mb;
x=a-b;
y=a+b;
output;
end;
return;
run;
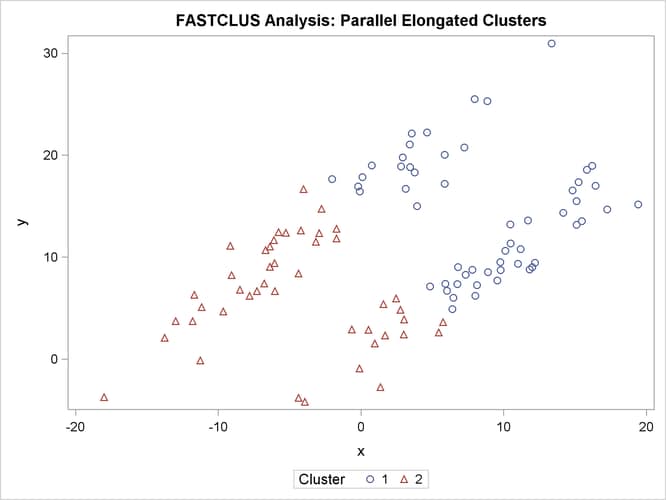
proc fastclus data=elongate out=out maxc=2 noprint; run; %modstyle(name=ClusterStyle2,parent=Statistical,type=CLM, markers=Circle Triangle circlefilled); ods listing style=ClusterStyle2; proc sgplot; scatter y=y x=x / group=cluster; title 'FASTCLUS Analysis: Parallel Elongated Clusters'; run;
Notice that PROC FASTCLUS found two clusters, as requested by the MAXC= option. However, it attempted to form spherical clusters, which are obviously inappropriate for these data.
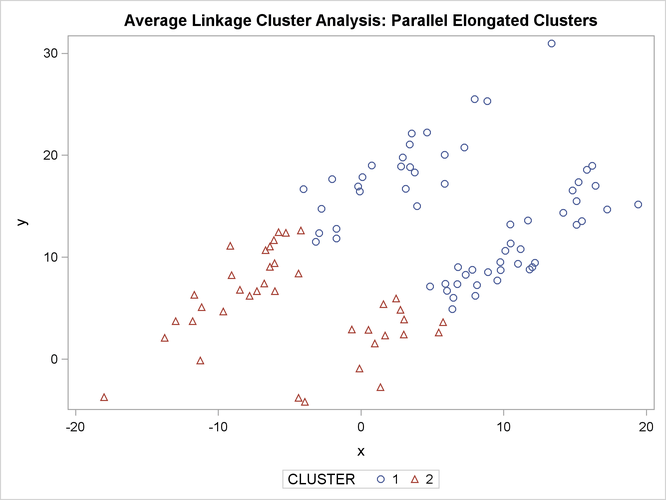
The following SAS statements produce Figure 11.19:
proc cluster data=elongate outtree=tree method=average noprint;
run;
proc tree noprint out=out n=2 dock=5;
copy x y;
run;
proc sgplot;
scatter y=y x=x / group=cluster;
title 'Average Linkage Cluster Analysis: '
'Parallel Elongated Clusters';
run;
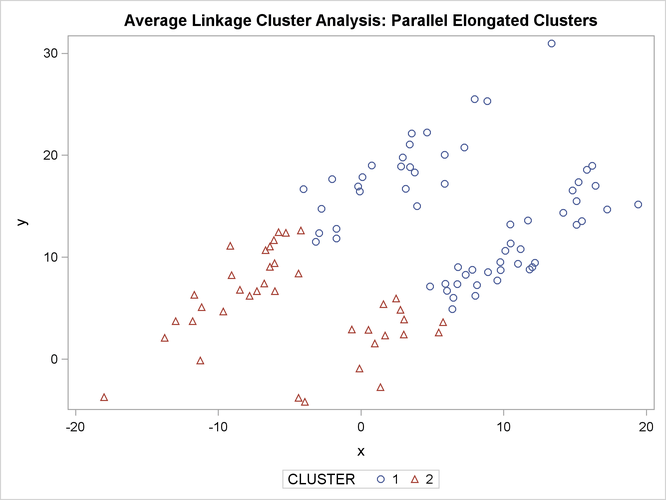
The following SAS statements produce Figure 11.20:
proc cluster data=elongate outtree=tree method=twostage k=10 noprint;
run;
proc tree noprint out=out n=2;
copy x y;
run;
proc sgplot;
scatter y=y x=x / group=cluster;
title 'Two-Stage Density Linkage Cluster Analysis: '
'Parallel Elongated Clusters';
run;
PROC FASTCLUS and average linkage fail miserably. Ward’s method and the centroid method (not shown) produce almost the same results. Two-stage density linkage, however, recovers the correct clusters. Single linkage (not shown) finds the same clusters as two-stage density linkage except for some outliers.
In this example, the population clusters have equal covariance matrices. If the within-cluster covariances are known, the data can be transformed to make the clusters spherical so that any of the clustering methods can find the correct clusters. But when you are doing a cluster analysis, you do not know what the true clusters are, so you cannot calculate the within-cluster covariance matrix. Nevertheless, it is sometimes possible to estimate the within-cluster covariance matrix without knowing the cluster membership or even the number of clusters, using an approach invented by Art, Gnanadesikan, and Kettenring (1982). A method for obtaining such an estimate is available in the ACECLUS procedure.
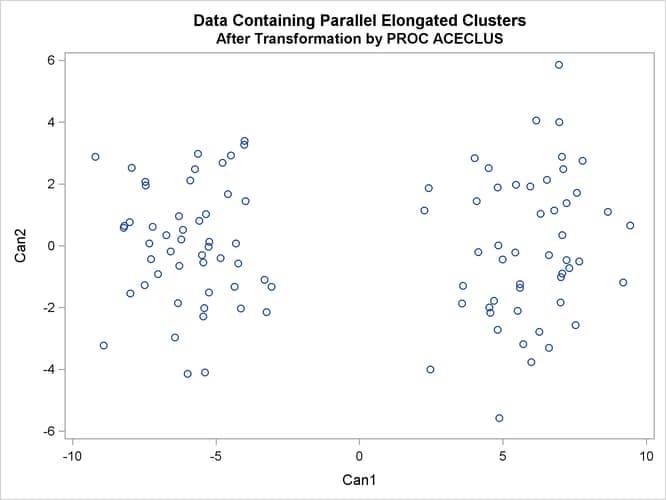
In the following analysis, PROC ACECLUS transforms the variables X and Y into the canonical variables Can1 and Can2. The latter are plotted and then used in a cluster analysis by Ward’s method. The clusters are then plotted with the original
variables X and Y.
The following SAS statements produce Figure 11.21 and Figure 11.22:
proc aceclus data=elongate out=ace p=.1; var x y; title 'ACECLUS Analysis: Parallel Elongated Clusters'; run; proc sgplot; scatter y=can2 x=can1; title 'Data Containing Parallel Elongated Clusters'; title2 'After Transformation by PROC ACECLUS'; run;
Figure 11.21: Parallel Elongated Clusters: PROC ACECLUS
| Iteration History | ||||
|---|---|---|---|---|
| Iteration | RMS Distance |
Distance Cutoff |
Pairs Within Cutoff |
Convergence Measure |
| 1 | 2.000 | 0.657 | 672.0 | 0.673685 |
| 2 | 9.382 | 3.082 | 716.0 | 0.006963 |
| 3 | 9.339 | 3.068 | 760.0 | 0.008362 |
| 4 | 9.437 | 3.100 | 824.0 | 0.009656 |
| 5 | 9.359 | 3.074 | 889.0 | 0.010269 |
| 6 | 9.267 | 3.044 | 955.0 | 0.011276 |
| 7 | 9.208 | 3.025 | 999.0 | 0.009230 |
| 8 | 9.230 | 3.032 | 1052.0 | 0.011394 |
| 9 | 9.226 | 3.030 | 1091.0 | 0.007924 |
| 10 | 9.173 | 3.013 | 1121.0 | 0.007993 |
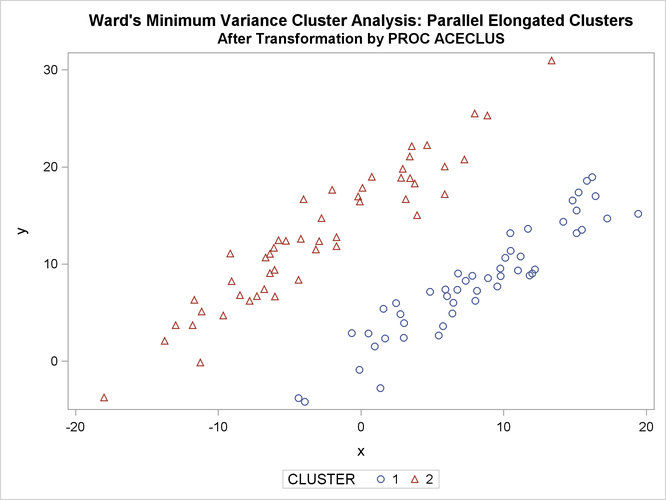
The following SAS statements produce Figure 11.23:
proc cluster data=ace outtree=tree method=ward noprint;
var can1 can2;
copy x y;
run;
proc tree noprint out=out n=2;
copy x y;
run;
proc sgplot;
scatter y=y x=x / group=cluster;
title 'Ward''s Minimum Variance Cluster Analysis: '
'Parallel Elongated Clusters';
title2 'After Transformation by PROC ACECLUS';
run;