Introduction to Bayesian Analysis Procedures
Bayesian methods and classical methods both have advantages and disadvantages, and there are some similarities. When the sample size is large, Bayesian inference often provides results for parametric models that are very similar to the results produced by frequentist methods. Some advantages to using Bayesian analysis include the following:
-
It provides a natural and principled way of combining prior information with data, within a solid decision theoretical framework. You can incorporate past information about a parameter and form a prior distribution for future analysis. When new observations become available, the previous posterior distribution can be used as a prior. All inferences logically follow from Bayes’ theorem.
-
It provides inferences that are conditional on the data and are exact, without reliance on asymptotic approximation. Small sample inference proceeds in the same manner as if one had a large sample. Bayesian analysis also can estimate any functions of parameters directly, without using the "plug-in" method (a way to estimate functionals by plugging the estimated parameters in the functionals).
-
It obeys the likelihood principle. If two distinct sampling designs yield proportional likelihood functions for
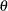 , then all inferences about
, then all inferences about 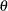 should be identical from these two designs. Classical inference does not in general obey the likelihood principle.
should be identical from these two designs. Classical inference does not in general obey the likelihood principle.
-
It provides interpretable answers, such as “the true parameter
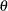 has a probability of 0.95 of falling in a 95% credible interval.”
has a probability of 0.95 of falling in a 95% credible interval.”
-
It provides a convenient setting for a wide range of models, such as hierarchical models and missing data problems. MCMC, along with other numerical methods, makes computations tractable for virtually all parametric models.
There are also disadvantages to using Bayesian analysis:
-
It does not tell you how to select a prior. There is no correct way to choose a prior. Bayesian inferences require skills to translate subjective prior beliefs into a mathematically formulated prior. If you do not proceed with caution, you can generate misleading results.
-
It can produce posterior distributions that are heavily influenced by the priors. From a practical point of view, it might sometimes be difficult to convince subject matter experts who do not agree with the validity of the chosen prior.
-
It often comes with a high computational cost, especially in models with a large number of parameters. In addition, simulations provide slightly different answers unless the same random seed is used. Note that slight variations in simulation results do not contradict the early claim that Bayesian inferences are exact. The posterior distribution of a parameter is exact, given the likelihood function and the priors, while simulation-based estimates of posterior quantities can vary due to the random number generator used in the procedures.
For more in-depth treatments of the pros and cons of Bayesian analysis, see Berger (1985, Sections 4.1 and 4.12), Berger and Wolpert (1988), Bernardo and Smith (1994, with a new edition coming out), Carlin and Louis (2000, Section 1.4), Robert (2001, Chapter 11), and Wasserman (2004, Section 11.9).
The following sections provide detailed information about the Bayesian methods provided in SAS.