The SURVEYMEANS Procedure

Variance and Standard Deviation of the Total

When you specify the keyword STD or the keyword SUM, the procedure estimates the standard deviation of the total. The keyword VARSUM requests the variance of the total.

Taylor Series Method

When you use VARMETHOD=TAYLOR, or by default, PROC SURVEYMEANS uses the Taylor series method to estimate the variance of the total as

$\widehat{V}(\widehat{Y}) = \sum _{h=1}^ H \widehat{V_ h}(\widehat{Y})$

where, if $n_ h>1$ , then

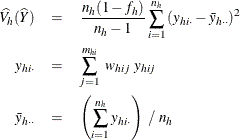
$\begin{eqnarray*} \widehat{V_ h}(\widehat{Y}) & =& \frac{n_ h(1-f_ h)}{n_ h-1} \sum _{i=1}^{n_ h} {(y_{hi\cdot }-\bar{y}_{h\cdot \cdot })^2} \\ y_{hi\cdot }& =& \sum _{j=1}^{m_{hi}} ~ w_{hij} ~ y_{hij}\\ \bar{y}_{h\cdot \cdot } & =& \left( \sum _{i=1}^{n_ h}y_{hi\cdot } \right) ~ / ~ n_ h \end{eqnarray*}$

and if $n_ h=1$ , then

$\widehat{V_ h}(\widehat{Y}) = \left\{ \begin{array}{ll} \mbox{missing} & \mbox{ if } n_{h}=1 \mbox{ for } h’=1, 2, \ldots , H \\ 0 & \mbox{ if } n_{h}>1 \mbox{ for some } 1 \le h’ \le H \end{array} \right.$

Replication Methods

When you specify VARMETHOD=BRR or VARMETHOD=JACKKNIFE option, the procedure computes the variance $\widehat{V}(\widehat{Y})$ with replication methods by measuring the variability among the estimates derived from these replicates. See the section Replication Methods for Variance Estimation for more details.

Standard Deviation

The standard deviation of the total equals

$\mbox{Std}(\widehat{Y})= \sqrt {\widehat{V}(\widehat{Y})}$