The SURVEYMEANS Procedure
For a stratified clustered sample design, together with the sampling weights, the sample can be represented by an ![]() matrix
matrix
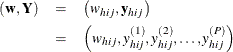
where
-
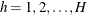 is the stratum index
is the stratum index
-
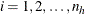 is the cluster index within stratum h
is the cluster index within stratum h
-
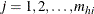 is the unit index within cluster i of stratum h
is the unit index within cluster i of stratum h
-
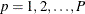 is the analysis variable number, with a total of P variables
is the analysis variable number, with a total of P variables
-
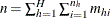 is the total number of observations in the sample
is the total number of observations in the sample
-
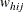 denotes the sampling weight for unit j in cluster i of stratum h
denotes the sampling weight for unit j in cluster i of stratum h
-
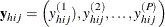 are the observed values of the analysis variables for unit j in cluster i of stratum h, including both the values of numerical variables and the values of indicator variables for levels of categorical variables.
are the observed values of the analysis variables for unit j in cluster i of stratum h, including both the values of numerical variables and the values of indicator variables for levels of categorical variables.
For a categorical variable
C, let l denote the number of levels of C, and denote the level values as ![]() . Let
. Let ![]()
![]() be an indicator variable for the category
be an indicator variable for the category ![]()
![]() with the observed value in unit j in cluster i of stratum h:
with the observed value in unit j in cluster i of stratum h:
Note that the indicator variable ![]() is set to missing when
is set to missing when ![]() is missing. Therefore, the total number of analysis variables, P, is the total number of numerical variables plus the total number of levels of all categorical variables.
is missing. Therefore, the total number of analysis variables, P, is the total number of numerical variables plus the total number of levels of all categorical variables.
The sampling rate ![]() for stratum h, which is used in Taylor series variance estimation, is the fraction of first-stage units (PSUs) selected for the sample.
You can use the TOTAL= or RATE= option to input population totals or sampling rates. See the section Specification of Population Totals and Sampling Rates for details. If you input stratum totals, PROC SURVEYMEANS computes
for stratum h, which is used in Taylor series variance estimation, is the fraction of first-stage units (PSUs) selected for the sample.
You can use the TOTAL= or RATE= option to input population totals or sampling rates. See the section Specification of Population Totals and Sampling Rates for details. If you input stratum totals, PROC SURVEYMEANS computes ![]() as the ratio of the stratum sample size to the stratum total. If you input stratum sampling rates, PROC SURVEYMEANS uses
these values directly for
as the ratio of the stratum sample size to the stratum total. If you input stratum sampling rates, PROC SURVEYMEANS uses
these values directly for ![]() . If you do not specify the TOTAL= or RATE= option, then the procedure assumes that the stratum sampling rates
. If you do not specify the TOTAL= or RATE= option, then the procedure assumes that the stratum sampling rates ![]() are negligible, and a finite population correction is not used when computing variances. Replication methods specified by
the VARMETHOD=BRR or the VARMETHOD=JACKKNIFE option do not use this finite population correction
are negligible, and a finite population correction is not used when computing variances. Replication methods specified by
the VARMETHOD=BRR or the VARMETHOD=JACKKNIFE option do not use this finite population correction ![]() .
.
