The most frequently used statistical methods are known as frequentist (or classical) methods. These methods assume that unknown parameters are fixed constants, and they define probability by using limiting relative frequencies. It follows from these assumptions that probabilities are objective and that you cannot make probabilistic statements about parameters because they are fixed. Bayesian methods offer an alternative approach; they treat parameters as random variables and define probability as “degrees of belief” (that is, the probability of an event is the degree to which you believe the event is true). It follows from these postulates that probabilities are subjective and that you can make probability statements about parameters. The term “Bayesian” comes from the prevalent usage of Bayes’ theorem, which was named after the Reverend Thomas Bayes, an eighteenth century Presbyterian minister. Bayes was interested in solving the question of inverse probability: after observing a collection of events, what is the probability of one event?
Suppose you are interested in estimating ![]() from data
from data ![]() by using a statistical model described by a density
by using a statistical model described by a density ![]() . Bayesian philosophy states that
. Bayesian philosophy states that ![]() cannot be determined exactly, and uncertainty about the parameter is expressed through probability statements and distributions.
You can say that
cannot be determined exactly, and uncertainty about the parameter is expressed through probability statements and distributions.
You can say that ![]() follows a normal distribution with mean 0 and variance 1, if it is believed that this distribution best describes the uncertainty
associated with the parameter. The following steps describe the essential elements of Bayesian inference:
follows a normal distribution with mean 0 and variance 1, if it is believed that this distribution best describes the uncertainty
associated with the parameter. The following steps describe the essential elements of Bayesian inference:
-
A probability distribution for
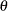 is formulated as
is formulated as 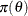 , which is known as the prior distribution, or just the prior.
The prior distribution expresses your beliefs (for example, on the mean, the spread, the skewness, and so forth) about the
parameter before you examine the data.
, which is known as the prior distribution, or just the prior.
The prior distribution expresses your beliefs (for example, on the mean, the spread, the skewness, and so forth) about the
parameter before you examine the data.
-
Given the observed data
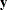 , you choose a statistical model
, you choose a statistical model 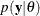 to describe the distribution of
to describe the distribution of 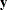 given
given 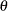 .
.
-
You update your beliefs about
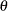 by combining information from the prior distribution and the data through the calculation of the posterior distribution,
by combining information from the prior distribution and the data through the calculation of the posterior distribution,
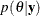 .
.
The third step is carried out by using Bayes’ theorem, which enables you to combine the prior distribution and the model in the following way:
The quantity
is the normalizing constant
of the posterior distribution. This quantity ![]() is also the marginal distribution of
is also the marginal distribution of ![]() ,
and it is sometimes called the marginal distribution of the data. The likelihood function
of
,
and it is sometimes called the marginal distribution of the data. The likelihood function
of ![]() is any function proportional to
is any function proportional to ![]() ; that is,
; that is, ![]() . Another way of writing Bayes’ theorem is as follows:
. Another way of writing Bayes’ theorem is as follows:
The marginal distribution ![]() is an integral. As long as the integral is finite, the particular value of the integral does not provide any additional information
about the posterior distribution. Hence,
is an integral. As long as the integral is finite, the particular value of the integral does not provide any additional information
about the posterior distribution. Hence, ![]() can be written up to an arbitrary constant, presented here in proportional form as:
can be written up to an arbitrary constant, presented here in proportional form as:
Simply put, Bayes’ theorem tells you how to update existing knowledge with new information. You begin with a prior belief
![]() , and after learning information from data
, and after learning information from data ![]() , you change or update your belief about
, you change or update your belief about ![]() and obtain
and obtain ![]() . These are the essential elements of the Bayesian approach to data analysis.
. These are the essential elements of the Bayesian approach to data analysis.
In theory, Bayesian methods offer simple alternatives to statistical inference—all inferences follow from the posterior distribution
![]() . In practice, however, you can obtain the posterior distribution with straightforward analytical solutions only in the most
rudimentary problems. Most Bayesian analyses require sophisticated computations, including the use of simulation methods.
You generate samples from the posterior distribution and use these samples to estimate the quantities of interest. PROC MCMC
uses a self-tuning Metropolis algorithm (see the section Metropolis and Metropolis-Hastings Algorithms). The GENMOD, LIFEREG, and PHREG procedures use the Gibbs sampler (see the section Gibbs Sampler). The BCHOICE and FMM procedure use a combination of Gibbs sampler and latent variable sampler. An important aspect of any
analysis is assessing the convergence of the Markov chains. Inferences based on nonconverged Markov chains can be both inaccurate
and misleading.
. In practice, however, you can obtain the posterior distribution with straightforward analytical solutions only in the most
rudimentary problems. Most Bayesian analyses require sophisticated computations, including the use of simulation methods.
You generate samples from the posterior distribution and use these samples to estimate the quantities of interest. PROC MCMC
uses a self-tuning Metropolis algorithm (see the section Metropolis and Metropolis-Hastings Algorithms). The GENMOD, LIFEREG, and PHREG procedures use the Gibbs sampler (see the section Gibbs Sampler). The BCHOICE and FMM procedure use a combination of Gibbs sampler and latent variable sampler. An important aspect of any
analysis is assessing the convergence of the Markov chains. Inferences based on nonconverged Markov chains can be both inaccurate
and misleading.
Both Bayesian and classical methods have their advantages and disadvantages. From a practical point of view, your choice of method depends on what you want to accomplish with your data analysis. If you have prior information (either expert opinion or historical knowledge) that you want to incorporate into the analysis, then you should consider Bayesian methods. In addition, if you want to communicate your findings in terms of probability notions that can be more easily understood by nonstatisticians, Bayesian methods might be appropriate. The Bayesian paradigm can often provide a framework for answering specific scientific questions that a single point estimate cannot sufficiently address. Alternatively, if you are interested only in estimating parameters based on the likelihood, then numerical optimization methods, such as the Newton-Raphson method, can give you very precise estimates and there is no need to use a Bayesian analysis. For further discussions of the relative advantages and disadvantages of Bayesian analysis, see the section Bayesian Analysis: Advantages and Disadvantages.