Suppose you are interested in testing whether an experimental drug produces a lower systolic blood pressure than a placebo does. Will 25 subjects per treatment group yield a satisfactory power for this test? From previous work, you expect that the blood pressure is 132 for the control group and 120 for the drug treatment group and that the standard deviation is 15 for both groups. You want to use a one-sided test with a significance level of 0.05. Because there are two independent groups and you are assuming that blood pressure is normally distributed, the two-sample t test is an appropriate analysis.
Start by creating a new project. Select →. In the New window, select from the list. The Two-Sample t test project window appears, with the Edit Properties page displayed.
On this page enter a name to describe the project and enter project properties. Click each tab on the Edit Properties page to enter the desired properties. You can also change tabs by clicking the or buttons. See Figure 76.3.
The description is used to identify this particular project in the Open and Delete windows. Type a description for your project in the Project: text box.
For this example, change the description to Experimental blood pressure drug with two groups, as shown in Figure 76.35.
For the two-sample t test analysis, you can choose to solve for power, sample size per group, or total sample size. Specify the desired quantity type on the Solve For tab.
Click the Solve For tab and select the option as shown in Figure 76.35. For information about solving for sample size, see the section Solving for Sample Size.
Click the Distribution tab to select a distribution option that specifies the underlying distribution for the test statistic, as shown in Figure 76.36.
For this example, you are interested in means rather than mean ratios, so select the option.
Click the Hypothesis tab to select the type of test; see Figure 76.37.
You can choose either a one- or two-sided test. If you do not know the direction of the effect (that is, whether it is positive or negative), the two-sided test is appropriate. If you know the effect’s direction, the one-sided test is appropriate. For the one-sided test, the alternative hypothesis is assumed to be in the same direction as the effect. If you specify a one-sided test and the effect is in the unexpected direction, the results of the analysis are invalid.
The option assumes that you know the correct direction of the test. Select the and options to explicitly indicate the direction of the one-sided test.
Because you are interested only in whether the experimental drug lowers blood pressure, select the option on the Hypothesis tab.
Click the Test tab to select either the pooled t test or the Satterthwaite t test.
With the independent variances that the example uses, select option. The Satterthwaite t test is used with unequal variances; it is available only with the normal distribution.
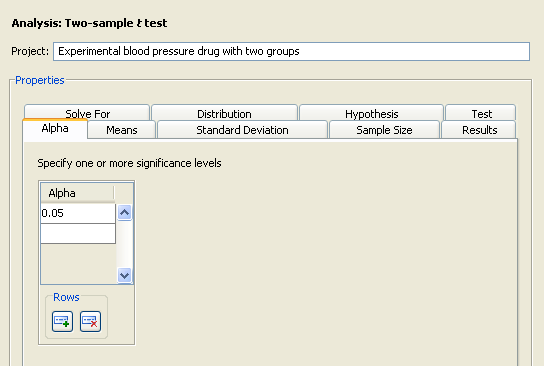
Click the Alpha tab to specify one or more significance levels, as shown in Figure 76.39.
Alpha is the significance level (that is, the probability of falsely rejecting the null hypothesis). If you frequently use the same values for alpha, set them as defaults in the Preferences window. See the section Setting Preferences for more information about setting preferences.
Type the desired significance level of 0.05 in the first cell of the Alpha table (if it is not already the default value).
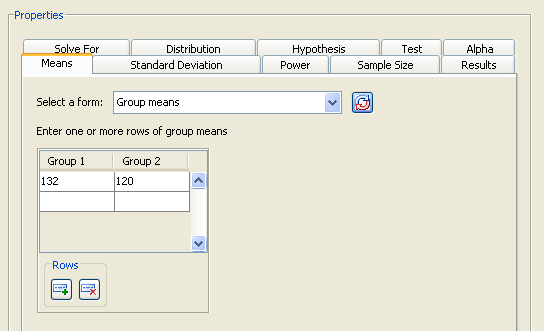
Click the Means tab to select one of four possible ways to enter the means and the null mean difference, as shown in Figure 76.40.
Select one of the following forms from the Select A Form list. The four available forms are:
-
Enter the difference between the group means. The null mean difference is assumed to be 0.
-
Enter the means for each group. The null mean difference is assumed to be 0. The difference is formed by subtracting the mean for group 1 from the mean for group 2.
-
Enter the difference between the group means and a null mean difference.
-
Enter the means for each group and a null mean difference. The difference is formed by subtracting the mean for group 1 from the mean for group 2.
For this analysis, you can enter the means for the two groups either individually or as a difference. If your null mean difference is not zero, enter that value in the Null Mean table. (The Null Mean table is displayed only for the and forms.)
For this example, a null mean difference of 0 is reasonable, so select the form from the list, as shown in Figure 76.40. Enter the control mean of 132 in the first row of the first column and the experimental mean of 120 in the first row of the second column.
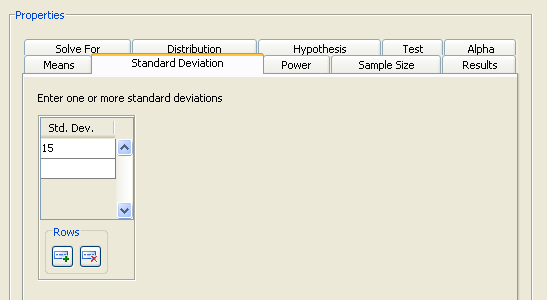
Click the Standard Deviation tab to enter the standard deviation for the two groups. It is assumed to be equal for both groups.
For the example, enter a single value of 15, as shown in Figure 76.41.
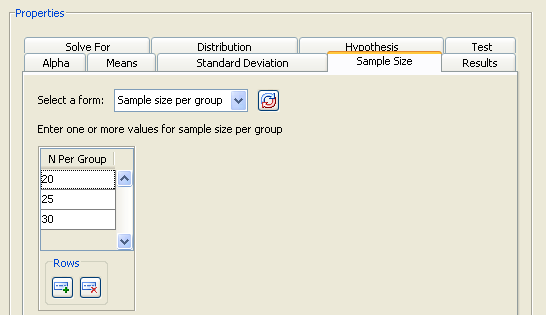
Click the Sample Size tab to select one of three possible ways to enter the sample sizes, as shown in Figure 76.40.
Select one of the following forms from the Select A Form list:
-
Enter the sample size for one of the two groups. The group sizes are assumed to be equal.
-
Enter the sample size for each of the two groups. The group sizes can be equal or unequal.
-
Enter the total sample size for the two groups and the relative sample sizes for each group. For more information about using relative sample sizes, see the section Using Unequal Group Sizes.
Examine the alternatives by clicking the Select a form down arrow. For this example, select the form. You want to examine a curve of powers in the power by sample size graph, so enter the values 20, 25, and 30 in the Sample Size table, as shown in Figure 76.42. If you need to add more rows to the table, add them by clicking the
 button beneath the table.
button beneath the table.
Table 76.2 contains the values of the input parameters for the example.
Table 76.2: Summary of Input Properties
|
Parameter |
Value |
|---|---|
|
Solve for |
Power |
|
Distribution |
Normal |
|
Hypothesis |
One-sided test |
|
Test |
Pooled t test |
|
Alpha |
0.05 |
|
Means form |
Group means |
|
Means |
132, 120 |
|
Standard deviation |
15 |
|
Sample size form |
Sample size per group |
|
Sample size |
20, 25, 30 |
Click the Results tab to request desired results. Summary table and power by sample size graph options are available.
For the example, select the and check boxes.
Click to perform the analysis. If there are no errors in the input values, the View Results page appears. If there are errors in the input parameter values, you are prompted to correct them.
The results are listed on separate tabs on the View Results page. Click the tab of each result that you want to view.
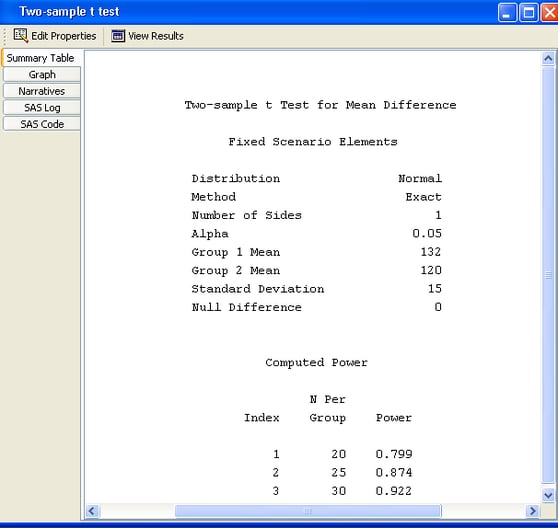
Click the Summary Table tab to view a table that includes the values of the input parameters and the computed quantity (in this example, power). See Figure 76.43.
The table consists of two subtables: the Fixed Scenario Elements table that contains the input parameters that have only one value for the analysis, and the Computed Power table that contains the input parameters that have more than one value for the analysis and the corresponding power. Only
the N per group parameter appears in the Computed Power table; all of the other input parameters have a single value. The computed power for a sample size per group of 25 is 0.874.
Thus, you have a probability of 0.87 that the study will find the expected result if the assumptions and conjectured values
are correct.
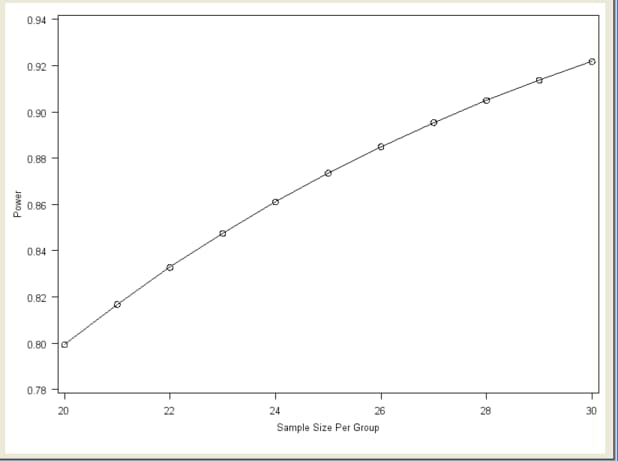
Click the Graph tab to view a power by sample size graph that displays power on the vertical axis and sample size per group on the horizontal axis. See Figure 76.44.
The range of values for the horizontal axis is 20 to 30, which were the smallest and largest values, respectively, that you entered on the Sample Size tab. You can customize the graph by specifying the values for the sample size axis (see the section Customizing Graphs).
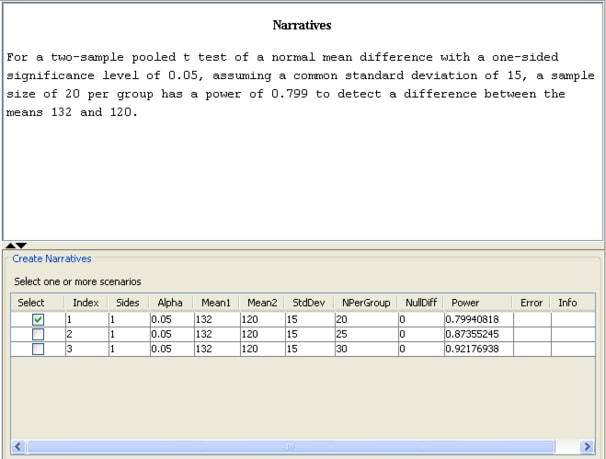
Click the Narratives tab to create and display a sentence- or paragraph-length text summary of the input parameter values and the computed quantity for combinations of the input parameter values; see Figure 76.45.
To create a narrative, selected the desired scenario (row) in the narrative selector table at the bottom of the Narratives tab.
In this example, select the narrative for the sample size per group of 20, which yields a power of 0.799. The following text summary is displayed:
For a two-sample pooled t test of a normal mean difference with a one-sided significance level of 0.05, assuming a common standard deviation of 15, a sample size of 20 per group has a power of 0.799 to detect a difference between the means 132 and 120.
To create other narratives, select the desired rows in the narrative selector table. If you also select the second row for the sample size of 25, another text summary is displayed below the first one:
For a two-sample pooled t test of a normal mean difference with a one-sided significance level of 0.05, assuming a common standard deviation of 15, a sample size of 20 per group has a power of 0.799 to detect a difference between the means 132 and 120. For a two-sample pooled t test of a normal mean difference with a one-sided significance level of 0.05, assuming a common standard deviation of 15, a sample size of 25 per group has a power of 0.874 to detect a difference between the means 132 and 120.
To change some values of the analysis and rerun it, select the Edit Properties page, change the desired properties, and click the button again.